题目内容
【题目】在极坐标系中,射线l:θ= ![]() 与圆C:ρ=2交于点A,椭圆Γ的方程为ρ2=
与圆C:ρ=2交于点A,椭圆Γ的方程为ρ2= ![]() ,以极点为原点,极轴为x轴正半轴建立平面直角坐标系xOy (Ⅰ)求点A的直角坐标和椭圆Γ的参数方程;
,以极点为原点,极轴为x轴正半轴建立平面直角坐标系xOy (Ⅰ)求点A的直角坐标和椭圆Γ的参数方程;
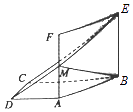
(Ⅱ)若E为椭圆Γ的下顶点,F为椭圆Γ上任意一点,求 ![]()
![]() 的取值范围.
的取值范围.
【答案】解:(Ⅰ)射线l:θ= ![]() 与圆C:ρ=2交于点A(2,
与圆C:ρ=2交于点A(2, ![]() ),点A的直角坐标(
),点A的直角坐标( ![]() ,1); 椭圆Γ的方程为ρ2=
,1); 椭圆Γ的方程为ρ2= ![]() ,直角坐标方程为
,直角坐标方程为 ![]() +y2=1,参数方程为
+y2=1,参数方程为 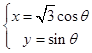 (θ为参数);
(θ为参数);
(Ⅱ)设F( ![]() cosθ,sinθ),
cosθ,sinθ),
∵E(0,﹣1),
∴ ![]() =(﹣
=(﹣ ![]() ,﹣2),
,﹣2), ![]() =(
=( ![]() cosθ﹣
cosθ﹣ ![]() ,sinθ﹣1),
,sinθ﹣1),
∴ ![]()
![]() =﹣3cosθ+3﹣2(sinθ﹣1)=
=﹣3cosθ+3﹣2(sinθ﹣1)= ![]() sin(θ+α)+5,
sin(θ+α)+5,
∴ ![]()
![]() 的取值范围是[5﹣
的取值范围是[5﹣ ![]() ,5+
,5+ ![]() ]
]
【解析】(Ⅰ)射线l:θ= ![]() 与圆C:ρ=2交于点A(2,
与圆C:ρ=2交于点A(2, ![]() ),可得点A的直角坐标;求出椭圆直角坐标方程,即可求出椭圆Γ的参数方程;(Ⅱ)设F(
),可得点A的直角坐标;求出椭圆直角坐标方程,即可求出椭圆Γ的参数方程;(Ⅱ)设F( ![]() cosθ,sinθ),E(0,﹣1),求出相应的向量,即可求
cosθ,sinθ),E(0,﹣1),求出相应的向量,即可求 ![]()
![]() 的取值范围.
的取值范围.

【题目】中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分儿口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料见如表:
井号I | 1 | 2 | 3 | 4 | 5 | 6 |
坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为y=6.5x+a,求a,并估计y的预报值;
(2)现准备勘探新井7(1,25),若通过1、3、5、7号井计算出的 ![]() 的值(
的值( ![]() 精确到0.01)相比于(1)中b,a的值之差不超过10%,则使用位置最接近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井? (参考公式和计算结果:
精确到0.01)相比于(1)中b,a的值之差不超过10%,则使用位置最接近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井? (参考公式和计算结果: 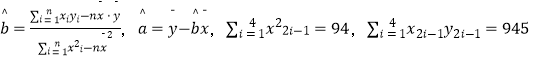 )
)
(3)设出油量与勘探深度的比值k不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.