Question

【题目】在等差数列{an}中，a1=﹣2，a12=20． （Ⅰ）求通项an；
（Ⅱ）若 ，求数列 的前n项和．

Answer 1

【答案】解：（Ⅰ）因为 an=﹣2+（n﹣1）d，

所以 a12=﹣2+11d=20．

于是 d=2，

所以 an=2n﹣4．

（Ⅱ）因为an=2n﹣4，

所以 ．

于是 ，

令 ，则 ．

显然数列{cn}是等比数列，且 ，公比q=3，

所以数列 的前n项和

【解析】（Ⅰ）根据等差数列的通项公式即可求出公差d，写出通项公式即可，（Ⅱ）先根据等差数列的求和公式化简bn，再判断数列 为等比数列，根据等比数列的求和公式计算即可．
【考点精析】通过灵活运用等差数列的通项公式（及其变式）和数列的前n项和，掌握通项公式：或；数列{an}的前n项和sn与通项an的关系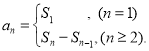即可以解答此题．