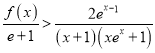题目内容
【题目】如图,三棱锥P﹣ABC,已知PA⊥面ABC,AD⊥BC于D,BC=CD=AD=1,设PD=x,∠BPC=θ,记函数f(x)=tanθ,则下列表述正确的是( ) 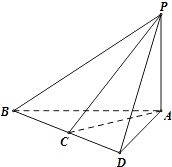
A.f(x)是关于x的增函数
B.f(x)是关于x的减函数
C.f(x)关于x先递增后递减
D.关于x先递减后递增
【答案】C
【解析】解:∵PA⊥平面ABC,AD⊥BC于D,BC=CD=AD=1,PD=x,∠BPC=θ,
∴可求得:AC= ![]() ,AB=
,AB= ![]() ,PA=
,PA= ![]() ,PC=
,PC= ![]() ,BP=
,BP= ![]() ,
,
∴在△PBC中,由余弦定理知:cosθ= ![]() =
= ![]()
∴tan2θ= ![]() ﹣1=
﹣1= ![]() ﹣1=
﹣1= ![]() ,
,
∴tanθ= ![]() =
= ![]() ≤
≤ ![]() =
= ![]() (当且仅当x=
(当且仅当x= ![]() 时取等号);
时取等号);
所以f(x)关于x先递增后递减.
故选:C.
【考点精析】本题主要考查了棱锥的结构特征和空间点、线、面的位置的相关知识点,需要掌握侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方;如果一条直线上的两点在一个平面内,那么这条直线在此平面内;过不在一条直线上的三点,有且只有一个平面;如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线(两个平面的交线);(平行线的传递性)平行与同一直线的两条直线互相平行才能正确解答此题.

练习册系列答案
相关题目