Question

【题目】动点与定点的距离和它到定直线的距离的比是∶，记点的轨迹为.

（1）求曲线的方程；

（2）对于定点，作过点的直线与曲线交于不同的两点，，求△的内切圆半径的最大值.

Answer 1

【答案】见解析

【解析】（1）由题意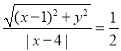，得，整理得，

所以曲线的方程为. ………………（4分）

（2）设，，又设的内切圆的半径为.

易知、为椭圆的左、右焦点，

所以的周长为，，

因此面积最大，就最大．

. ………………（6分）

由题意知，直线的斜率不为零，可设直线的方程为，

由，得，

所以，，． ………………（8分）

又因直线与椭圆交于不同的两点，

所以，即（），则．

令，则，． ………………（10分）

令，则.

所以函数在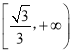上是单调递增函数，

即当时，在上单调递增，

因此有，所以，

即当，时，最大，此时，

故当直线的方程为时，内切圆半径的最大值为． ………………（12分）

【命题意图】本小题主要考查轨迹方程的求法、直线与椭圆的位置关系等基础知识，考查推理论证能力、运算求解能力，考查数形结合、转化与化归、分类与整合等数学思想，并考查思维的严谨性．