Question

【题目】已知数列{an}中，a1=1，a2= ，且an+1= （n=2，3，4…）．
（1）求数列{an}的通项公式；
（2）求证：对一切n∈N* ， 有 ＜ ．

Answer 1

【答案】
（1）解：∵a1=1，a2= ，且an+1= （nkkk=2，3，4…），

∴当n≥2时， = ，

两边同时除以n，得 ，

∴ =﹣（ ），

∴ =﹣ =﹣（1﹣ ）

∴ =﹣（1﹣ ），n≥2，

∴ ，

∴an= ，n≥2，

当n=1时，上式成立，

∴an= ，n∈N*

（2）证明：当k≥2时， = ，

∴当n≥2时，

=1+ ＜1+ [（ ）+（ ）+…+（ ）]

=1+ ＜1+ = ，

又n=1时， ，

∴对一切n∈N*，有 ak2＜

【解析】（1）当n≥2时， = ，从而 =﹣（ ），进而得到 =﹣（1﹣ ），由此能求出an= ，n∈N* ． （2）当k≥2时， = ，由此利用裂项求和法能证明对一切n∈N* ， 有 ＜ ．
【考点精析】通过灵活运用数列的前n项和和数列的通项公式，掌握数列{an}的前n项和sn与通项an的关系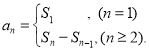；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式即可以解答此题．