题目内容
若数列{an}满足:存在正整数T,对于任意正整数n都有an+T=an成立,则称数列{an}为周期数列,周期为T.已知数列{an}满足a1=m(m>0),an+1=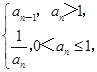 则下列结论中错误的是( )
则下列结论中错误的是( )
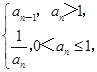 则下列结论中错误的是( )
则下列结论中错误的是( ) A.若m=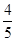 ,则a5=3 ,则a5=3 |
| B.若a3=2,则m可以取3个不同的值 |
C.若m=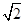 ,则数列{an}是周期为3的数列 ,则数列{an}是周期为3的数列 |
| D.?m∈Q且m≥2,使得数列{an}是周期数列 |
D
对于A,当a1=m=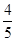 时,a2=
时,a2= ,a3=a2-1=
,a3=a2-1= ,a4=4,a5=3,因此选项A正确.对于B,当a3=2时,若a2>1,则a3=a2-1=2,a2=3,
,a4=4,a5=3,因此选项A正确.对于B,当a3=2时,若a2>1,则a3=a2-1=2,a2=3, 或
或 由此解得m=4或m=
由此解得m=4或m= ;若0<a2≤1,则a3=
;若0<a2≤1,则a3= =2,a2=
=2,a2= ,
, 或
或 由此解得m=
由此解得m= ,因此m的可能值是
,因此m的可能值是 ,
, ,4,选项B正确.对于C,当m=
,4,选项B正确.对于C,当m=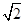 时,a1=
时,a1=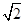 ,a2=
,a2=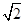 -1,a3=
-1,a3=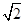 +1,a4=
+1,a4=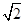 ,a5=
,a5=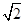 -1,a6=
-1,a6=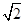 +1,…,此时数列{an}是以3为周期的数列,因此选项C正确.综上所述,故选D
+1,…,此时数列{an}是以3为周期的数列,因此选项C正确.综上所述,故选D
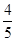 时,a2=
时,a2= ,a3=a2-1=
,a3=a2-1= ,a4=4,a5=3,因此选项A正确.对于B,当a3=2时,若a2>1,则a3=a2-1=2,a2=3,
,a4=4,a5=3,因此选项A正确.对于B,当a3=2时,若a2>1,则a3=a2-1=2,a2=3, 或
或 由此解得m=4或m=
由此解得m=4或m= ;若0<a2≤1,则a3=
;若0<a2≤1,则a3= =2,a2=
=2,a2= ,
, 或
或 由此解得m=
由此解得m= ,因此m的可能值是
,因此m的可能值是 ,
, ,4,选项B正确.对于C,当m=
,4,选项B正确.对于C,当m=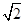 时,a1=
时,a1=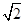 ,a2=
,a2=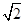 -1,a3=
-1,a3=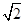 +1,a4=
+1,a4=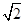 ,a5=
,a5=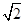 -1,a6=
-1,a6=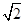 +1,…,此时数列{an}是以3为周期的数列,因此选项C正确.综上所述,故选D
+1,…,此时数列{an}是以3为周期的数列,因此选项C正确.综上所述,故选D
练习册系列答案
相关题目
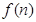 个小正方形.则
个小正方形.则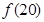 等于( )
等于( )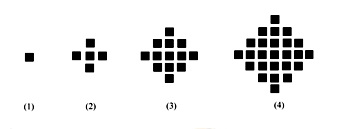
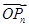 ·OPn+1的最小值;
·OPn+1的最小值;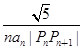 (n≥2),求c2+c3+c4+…+cn的值.
(n≥2),求c2+c3+c4+…+cn的值.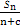 ,求非零常数c.
,求非零常数c.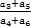 的值为( )
的值为( )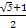


 的前
的前 项积记为
项积记为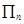 ,若
,若 ,则
,则 ( )
( )