题目内容
已知数列{an}满足an+1=an-an-1(n≥2),a1=1,a2=3,记Sn=a1+a2+…+an,则下列结论正确的是( )
| A.a100=-1,S100=5 | B.a100=-3,S100=5 |
| C.a100=-3,S100=2 | D.a100=-1,S100=2 |
A
依题意an+2=an+1-an=-an-1,即an+3=-an,an+6=-an+3=an,故数列{an}是以6为周期的数列,,a1+a2+a3+a4+a5+a6=(a1+a4)+(a2+a5)+(a3+a6)=0.注意到100=6×16+4,因此有a100=a4=-a1=-1,S100=16(a1+a2+…+a6)+(a1+a2+a3+a4)=a2+a3=a2+(a2-a1)=2×3-1=5,故选A

练习册系列答案
相关题目
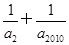 的最小值为________.
的最小值为________.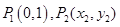 ,……,
,……,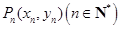 .若点
.若点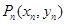 到点
到点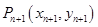 的变化关系为:
的变化关系为: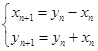
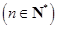 ,则
,则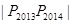 等于 .
等于 .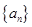 中,已知
中,已知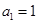 ,
,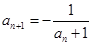 ,记
,记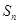 为数列
为数列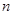 项和,则
项和,则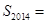 .
.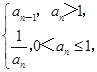 则下列结论中错误的是( )
则下列结论中错误的是( ) 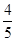 ,则a5=3
,则a5=3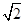 ,则数列{an}是周期为3的数列
,则数列{an}是周期为3的数列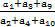 =( )
=( )