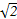题目内容
已知公差大于零的等差数列{an}的前n项和为Sn,且满足:a3·a4=117,a2+a5=22.
(1)求数列{an}的通项公式an.
(2)若数列{bn}是等差数列,且bn=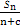 ,求非零常数c.
,求非零常数c.
(1)求数列{an}的通项公式an.
(2)若数列{bn}是等差数列,且bn=
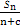 ,求非零常数c.
,求非零常数c.(1) n= 4n-3 (2)c=-

(1)由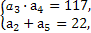 得
得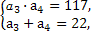
解得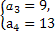 或
或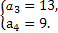
∵公差d>0,∴a3=9,a4=13,∴d=4.
∴an=a3+(n-3)d=9+(n-3)·4=4n-3.
(2)Sn=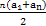 =
=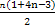 =2n2-n.
=2n2-n.
bn=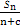 =
=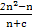 .
.
∵{bn}是等差数列,
∴b1+b3=2b2.
∴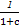 +
+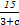 =2·
=2·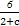 ,
,
∴2c2+c=0.
∵c≠0,∴c=- ,经检验c=-
,经检验c=- 符合题意.
符合题意.
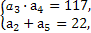 得
得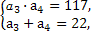
解得
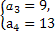 或
或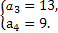
∵公差d>0,∴a3=9,a4=13,∴d=4.
∴an=a3+(n-3)d=9+(n-3)·4=4n-3.
(2)Sn=
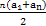 =
=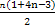 =2n2-n.
=2n2-n.bn=
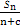 =
=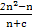 .
.∵{bn}是等差数列,
∴b1+b3=2b2.
∴
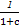 +
+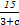 =2·
=2·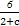 ,
,∴2c2+c=0.
∵c≠0,∴c=-
 ,经检验c=-
,经检验c=- 符合题意.
符合题意.
练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 )=4x-
)=4x- +1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).
+1,数列{an}和{bn}满足下列条件:a1=1,an+1-2an=f(n),bn=an+1-an(n∈N*).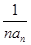 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.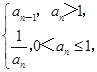 则下列结论中错误的是( )
则下列结论中错误的是( ) 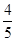 ,则a5=3
,则a5=3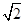 ,则数列{an}是周期为3的数列
,则数列{an}是周期为3的数列 <-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( )
<-1,且它的前n项和Sn有最大值,则使得Sn<0的n的最小值为( )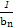 }的前n项和Tn.
}的前n项和Tn.