题目内容
3.设a=($\frac{3}{4}$)${\;}^{\frac{2}{3}}$,b=($\frac{2}{3}$)${\;}^{\frac{3}{4}}$,c=log${\;}_{\frac{2}{3}}$$\frac{4}{3}$,则a,b,c的大小关系是( )| A. | a>c>b | B. | a>b>c | C. | c>b>a | D. | b>c>a |
分析 根据指数幂和对数的性质分别进行判断即可.
解答 解:a=($\frac{3}{4}$)${\;}^{\frac{2}{3}}$>($\frac{2}{3}$)${\;}^{\frac{2}{3}}$>($\frac{2}{3}$)${\;}^{\frac{3}{4}}$>0,
即a>b,
c=log${\;}_{\frac{2}{3}}$$\frac{4}{3}$<0,
即a>b>c,
故选:B
点评 本题主要考查函数值的大小比较,根据指数幂和对数的性质是解决本题的关键.

练习册系列答案
相关题目
11.由直线y=x-4,曲线y=$\sqrt{2x}$以及y=0所围成的图形的面积为( )
| A. | $\frac{40}{3}$ | B. | $\frac{34}{3}$ | C. | $\frac{64}{3}$ | D. | 16 |
8.求值:sin45°cos15°+cos45°sin 15°=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
12.函数y=log2x+logx(2x)的值域为( )
| A. | (-∞,-1] | B. | [3,+∞) | C. | [1,3] | D. | (-∞,-1]∪[3,+∞) |
13.在平面直角坐标系中,不等式组$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y+2≥0}\\{y≥0}\end{array}\right.$表示的平面区域的面积是( )
| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
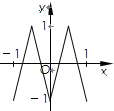
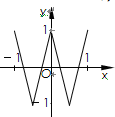
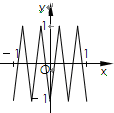
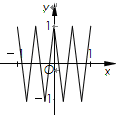
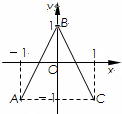 如图,函数y=f(x)的图象为折线ABC,设g(x)=f[f(x)],则函数y=g(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设g(x)=f[f(x)],则函数y=g(x)的图象为( )