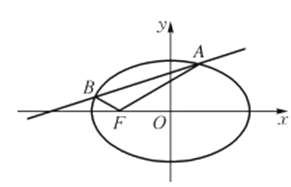
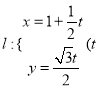题目内容
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,求证:对任意的
时,求证:对任意的![]() .
.
【答案】(1)![]() 在
在![]() 上是单调递减的函数;(2)详见解析.
上是单调递减的函数;(2)详见解析.
【解析】试题分析:(1)求导,根据导函数的取值情况分析![]() 的单调性;(2)令
的单调性;(2)令![]() ,求导,分析其单调性,进而研究其取值情况,问题等价于证明
,求导,分析其单调性,进而研究其取值情况,问题等价于证明![]() 即可得证..
即可得证..
试题解析:(1)当![]() 时,
时, ![]() ,
, ![]() ,
,
![]() ,∵当
,∵当![]() 时,
时, ![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上是单调递减的函数;(2)设
上是单调递减的函数;(2)设![]() ,
, ![]() ,
, ![]() ,令
,令![]() ,
, ![]() 则
则![]() ,当
,当![]() 时,
时, ![]() ,有
,有![]() ,∴
,∴![]() 在
在![]() 上是减函数,即
上是减函数,即![]() 在
在![]() 上是减函数,
上是减函数,
又∵![]() ,
,  ,∴
,∴![]() 存在唯一的
存在唯一的![]() ,使得
,使得![]() , ∴当
, ∴当![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 在区间
在区间![]() 单调递减,因此在区间
单调递减,因此在区间![]() 上
上
![]() ,
,
∵![]() ,∴
,∴![]() ,将其代入上式得
,将其代入上式得
![]() ,
,
令![]() ,
, ![]() ,则
,则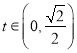 ,即有
,即有![]() ,
, 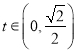 ,
,
∵![]() 的对称轴
的对称轴![]() ,∴函数
,∴函数![]() 在区间
在区间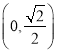 上是增函数,且
上是增函数,且![]() ,
,
∴ ,(
,( ![]() ),即任意
),即任意![]() ,
, ![]() ,∴
,∴![]() ,因此任意
,因此任意![]() ,
, ![]() .
.

【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在[25,35)和[55,65)的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在[55,65)的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: ![]() (其中
(其中![]() )
)