题目内容
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为矩形,E为PD上一点,AD=2AB=2AP=2,PE=2DE.

(1)若F为PE的中点,求证:BF∥平面ACE;
(2)求三棱锥P-ACE的体积.

(1)若F为PE的中点,求证:BF∥平面ACE;
(2)求三棱锥P-ACE的体积.
(1)见解析(2)

(1)证明:连接BD,交AC于点O,连接OE,

∵底面ABCD为矩形,∴OB=OD.
∵F为PE的中点,∴PE=2EF.
又∵PE=2DE,∴DE=EF,∴OE∥BF.
又∵BF?平面ACE,OE?平面ACE,∴BF∥平面ACE.
(2)∵侧棱PA⊥底面ABCD,∴AP⊥CD.
又∵底面ABCD为矩形,∴CD⊥AD.
∵AD∩AP=A,∴CD⊥平面PAD.
又∵AD=2AB=2AP=2,
∴VP-ACE=VC-AEP= ×CD×S△AEP=
×CD×S△AEP= ×CD×
×CD× S△ADP
S△ADP
= ×CD×AD×AP=
×CD×AD×AP= .
.

∵底面ABCD为矩形,∴OB=OD.
∵F为PE的中点,∴PE=2EF.
又∵PE=2DE,∴DE=EF,∴OE∥BF.
又∵BF?平面ACE,OE?平面ACE,∴BF∥平面ACE.
(2)∵侧棱PA⊥底面ABCD,∴AP⊥CD.
又∵底面ABCD为矩形,∴CD⊥AD.
∵AD∩AP=A,∴CD⊥平面PAD.
又∵AD=2AB=2AP=2,
∴VP-ACE=VC-AEP=
 ×CD×S△AEP=
×CD×S△AEP= ×CD×
×CD× S△ADP
S△ADP=
 ×CD×AD×AP=
×CD×AD×AP= .
.
练习册系列答案
相关题目
 ABCD的三视图如图所示,四棱锥P
ABCD的三视图如图所示,四棱锥P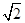 ,则该球表面积为( )
,则该球表面积为( )



 的矩形,则该正方体的正视图的面积等于( )
的矩形,则该正方体的正视图的面积等于( )

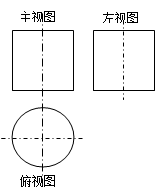




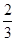 ,则其侧视图的面积为( )
,则其侧视图的面积为( )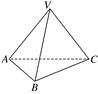






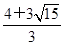 π
π π
π