题目内容
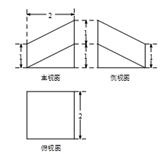
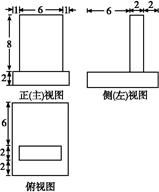
四棱锥P ABCD的三视图如图所示,四棱锥P
ABCD的三视图如图所示,四棱锥P ABCD的五个顶点都在一个球面上,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为2
ABCD的五个顶点都在一个球面上,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为2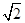 ,则该球表面积为( )
,则该球表面积为( )

(A)12π (B)24π (C)36π (D)48π
 ABCD的三视图如图所示,四棱锥P
ABCD的三视图如图所示,四棱锥P ABCD的五个顶点都在一个球面上,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为2
ABCD的五个顶点都在一个球面上,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为2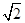 ,则该球表面积为( )
,则该球表面积为( )
(A)12π (B)24π (C)36π (D)48π
A
由三视图可知,四棱锥的直观图如图所示,

补成长方体后可知其外接球的球心是PC的中点,由题意可知正方形ABCD的外接圆的直径AC=2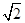 .即
.即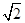 a=2
a=2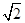 ,
,
∴a=2.
∴PA=2,
∴PC= =2
=2 ,
,
∴S球=4π·R2=4π·( )2=12π.
)2=12π.

补成长方体后可知其外接球的球心是PC的中点,由题意可知正方形ABCD的外接圆的直径AC=2
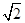 .即
.即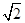 a=2
a=2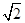 ,
,∴a=2.
∴PA=2,
∴PC=
 =2
=2 ,
,∴S球=4π·R2=4π·(
 )2=12π.
)2=12π.
练习册系列答案
相关题目

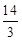
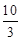



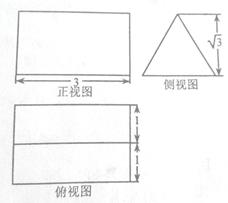


 的三视图如图所示,则四棱锥
的三视图如图所示,则四棱锥

 (AC+BD) (B)MN≤
(AC+BD) (B)MN≤ ,则该二面角的大小为 .
,则该二面角的大小为 .