Question

9．如图，在平面直角坐标系xoy中，椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{{\sqrt{6}}}{3}$，直线l与x轴交于点E，与椭圆C交于A、B两点．当直线l垂直于x轴且点E为椭圆C的右焦点时，弦AB的长为$\frac{{2\sqrt{6}}}{3}$．
（1）求椭圆C的方程；
（2）若点E的坐标为$（\frac{{\sqrt{3}}}{2}，0）$，点A在第一象限且横坐标为$\sqrt{3}$，
连结点A与原点O的直线交椭圆C于另一点P，求△PAB的面积．

Answer 1

分析 （1）由$\frac{c}{a}=\frac{{\sqrt{6}}}{3}$，设a=3k（k＞0），得$c=\sqrt{6}k$，把b²用k表示，得到椭圆方程$\frac{x^2}{{9{k^2}}}+\frac{y^2}{{3{k^2}}}=1$，再由已知条件求得k，则椭圆C的方程可求；
（2）将$x=\sqrt{3}$代入$\frac{x^2}{6}+\frac{y^2}{2}=1$，解得y=±1，进一步求出点A的坐标再由E$（\frac{{\sqrt{3}}}{2}，0）$，求出PA所在直线方程，与椭圆C的方程联立求得$B（-\frac{{\sqrt{3}}}{5}，-\frac{7}{5}）$，求出PA所在直线方程，可得点B到直线PA的距离，代入三角形面积公式得答案．

解答 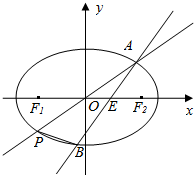解：（1）由$\frac{c}{a}=\frac{{\sqrt{6}}}{3}$，设a=3k（k＞0），则$c=\sqrt{6}k$，b²=3k²，
∴椭圆C的方程为$\frac{x^2}{{9{k^2}}}+\frac{y^2}{{3{k^2}}}=1$，
∵直线l垂直于x轴且点E为椭圆C的右焦点，即${x_A}={x_B}=\sqrt{6}k$，
代入椭圆方程，解得y=±k，
于是$2k=\frac{{2\sqrt{6}}}{3}$，即$k=\frac{{\sqrt{6}}}{3}$，
∴椭圆C的方程为$\frac{x^2}{6}+\frac{y^2}{2}=1$；
（2）将$x=\sqrt{3}$代入$\frac{x^2}{6}+\frac{y^2}{2}=1$，解得y=±1，
∵点A在第一象限，从而$A（\sqrt{3}，1）$，
由点E的坐标为$（\frac{{\sqrt{3}}}{2}，0）$，
∴${k_{AB}}=\frac{2}{{\sqrt{3}}}$，直线PA的方程为$y=\frac{2}{{\sqrt{3}}}（x-\frac{{\sqrt{3}}}{2}）$，
联立直线PA与椭圆C的方程，解得$B（-\frac{{\sqrt{3}}}{5}，-\frac{7}{5}）$，
又PA过原点O，于是$P（-\sqrt{3}，-1）$，PA=4，
∴直线PA的方程为$x-\sqrt{3}y=0$，
则点B到直线PA的距离$h=\frac{{|{-\frac{{\sqrt{3}}}{5}+\frac{{7\sqrt{3}}}{5}}|}}{2}=\frac{{3\sqrt{3}}}{5}$，
故${S_{△PAB}}=\frac{1}{2}•4•\frac{{3\sqrt{3}}}{5}=\frac{{6\sqrt{3}}}{5}$．

点评 本题考查椭圆的简单性质，考查了椭圆方程的求法，训练了点到直线的距离公式的应用，是中档题．