题目内容
【题目】某单位建造一间地面面积为12m2的背面靠墙的矩形小房子，由于地理位置的限制，房子侧面的长度x不得超过am．房屋正面的造价为400元/m2 ， 房屋侧面的造价为150元/m2 ， 屋顶和地面的造价费用合计为5800元，如果墙高为3m，且不计房屋背面的费用．当侧面的长度为多少时，总造价最低？
【答案】解：设总造价为Z元，则xy=12，有y= 
∴Z=3y×400+6x×150+5800
=900（x+ 
）+5800
≥900×2 
+5800
=13000 …（6分）
当 x= 时，即x=4时，Z有最小值13000，
若a≥4时，则x=4总进价最低，最低总造价是13000元．
当0＜a＜4时，则y′=900（1﹣ 
）
∴当0＜x＜4时，y′＜0，故函数y=900（x+ ）+5800（0，a]上是减函数，
∴当x=a时，y有最小值，即最低总造价为900（a+ 
）+5800元
答：当a≥4时，x=4总造价最低，最低总造价是13000元；
当0＜a＜4时，x=a总造价最低，最低总造价为900（a+ ）+5800元．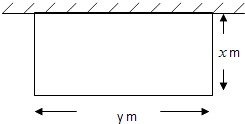
【解析】已知中地面面积为12m2 ， 我们可得xy=12有y= 
，根据房屋正面的造价为400元/m2 ， 房屋侧面的造价为150元/m2 ， 屋顶的造价共5200元，结合墙高为3m，我们可以构造房屋总造价的函数解析式，利用基本不等式或导数即可求出函数的最小值，进而得到答案．
练习册系列答案
应用题作业本系列答案
相关题目
