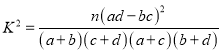题目内容
【题目】在![]() 中,内角A,B,C的对边分别是a,b,c,且a2+b2+
中,内角A,B,C的对边分别是a,b,c,且a2+b2+![]() ab=c2.
ab=c2.
(1)求C;
(2)设cos Acos B=![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)1或4.
;(2)1或4.
【解析】(1)因为a2+b2+![]() ab=c2,
ab=c2,
所以由余弦定理有cos C=![]() ,
,
故![]() .
.
(2)由题意得![]() =
=![]() ,
,
因此(tan αsin Acos A)(tan αsin Bcos B)=![]() ,
,
即tan2αsin Asin Btan α(sin Acos B+cos Asin B)+cos Acos B=![]() ,
,
即tan2αsin Asin Btan αsin(A+B)+cos Acos B=![]() ①.
①.
因为![]() ,
,
所以A+B=![]() ,
,
所以sin(A+B)=![]() .
.
因为cos(A+B)=cos Acos Bsin Asin B,即![]() -sin Asin B=
-sin Asin B=![]() ,
,
则sin Asin B=![]() .
.
代入①得tan2α5tan α+4=0,解得tan α=1或tan α=4.

 名校课堂系列答案
名校课堂系列答案【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,试估计该校学生每周平均体育运动时间超过4小时的概率.
,试估计该校学生每周平均体育运动时间超过4小时的概率.
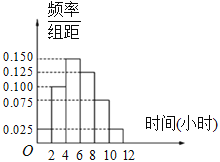
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时.请完成每周平均体育运动时间与性别的列联表,并判断能否在犯错误的概率不超过0.05的前提下认为该校学生的每周平均体育运动时间与性别有关?
男生 | 女生 | 合计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
合计 | 300 |
附:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:
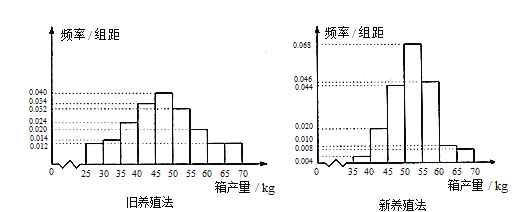
(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附: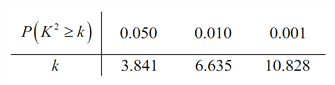 ,
,