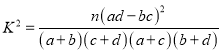题目内容
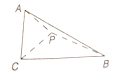
【题目】已知直角三角形![]() 的两条直角边
的两条直角边![]() ,
, ![]() ,
, ![]() 为斜边
为斜边![]() 上一点,沿
上一点,沿![]() 将三角形折成直二面角
将三角形折成直二面角![]() ,此时二面角
,此时二面角![]() 的正切值为
的正切值为![]() ,则翻折后
,则翻折后![]() 的长为( )
的长为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
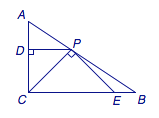
【解析】如图,在平面![]() 内过
内过![]() 作直二面角
作直二面角![]() 的棱
的棱![]() 的垂线交边
的垂线交边![]() 于
于![]() ,则
,则![]() .
.
于是在平面![]() 中过
中过![]() 作二面角
作二面角![]() 的棱
的棱![]() 的垂线,垂足为
的垂线,垂足为![]() ,连接
,连接![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,且
的平面角,且![]() ,设
,设![]() ,则
,则![]() .
.
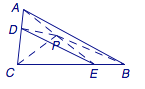
如图,设![]() ,则
,则![]() ,则在直角三角形
,则在直角三角形![]() 中,
中, 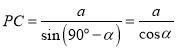 ,又在直角三角形
,又在直角三角形![]() 中,
中, ![]() 则
则![]() ,
, ![]() 所以
所以![]() ,因为二面角
,因为二面角![]() 为直二面角, 所以
为直二面角, 所以![]() ,于是
,于是![]() ,解得
,解得![]() . 选D.
. 选D.
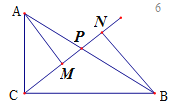
解法二:由![]() 得
得![]() ,翻折后
,翻折后![]() ,故
,故![]()
点睛:立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.二面角的寻找,主要找面的垂线,即需从线面垂直(本题利用面面垂直性质定理)出发,利用三垂线定理及其逆定理作出二面角的平面角.

【题目】某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,试估计该校学生每周平均体育运动时间超过4小时的概率.
,试估计该校学生每周平均体育运动时间超过4小时的概率.
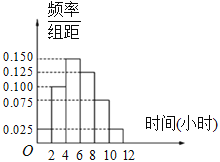
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时.请完成每周平均体育运动时间与性别的列联表,并判断能否在犯错误的概率不超过0.05的前提下认为该校学生的每周平均体育运动时间与性别有关?
男生 | 女生 | 合计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
合计 | 300 |
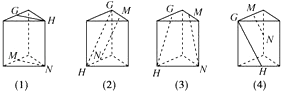
附:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:
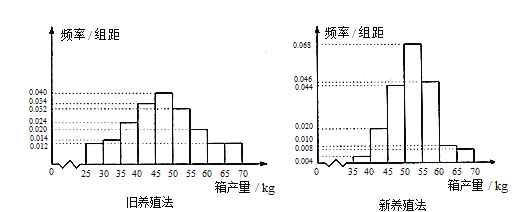
(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附: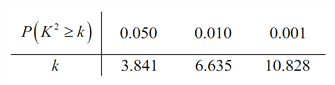 ,
,