题目内容
【题目】已知命题P：方程x2+mx+1=0有两个不等的实数根，命题q：方程4x2+4（m﹣2）x+1=0无实数根．若p∧q为假，若p∨q为真，求m的取值范围．
【答案】解：P真：△=m2﹣4＞0m＞2或m＜﹣2；
Q真：△=16（m﹣2）2﹣16＜0﹣1＜m﹣2＜11＜m＜3；
若P∨Q为真，P∧Q为假，则有P真Q假或Q真P假．
当P真Q假时， 
m＜﹣2或m≥3；
当P假Q真时， 
1＜m≤2；
∴满足题意的实数m的取值范围为：m＜﹣2或1＜m≤2或m≥3
【解析】根据题意，可分别求得P真与Q真时m的范围，再根据复合命题间的关系分P真Q假与P假Q真两类讨论即可求得实数m的取值范围．
【考点精析】认真审题，首先需要了解复合命题的真假(“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反；“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；“p或q”形式复合命题当p与q同为假时为假，其他情况时为真)．
【题目】某高校共有15000人，其中男生10500人，女生4500人，为调查该校学生每周平均体育运动时间的情况，采用分层抽样的方法，收集300位学生每周平均体育运动时间的样本数据（单位：小时）.
（1）应收集多少位女生的样本数据？
（2）根据这300个样本数据，得到学生每周平均体育运动时间的频率分布直方图（如图所示），其中样本数据分组区间为：
，试估计该校学生每周平均体育运动时间超过4小时的概率.
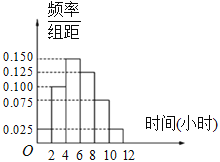
（3）在样本数据中，有60位女生的每周平均体育运动时间超过4小时.请完成每周平均体育运动时间与性别的列联表，并判断能否在犯错误的概率不超过0.05的前提下认为该校学生的每周平均体育运动时间与性别有关？
男生 | 女生 | 合计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
合计 | 300 |
附：
，其中
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
