题目内容
已知曲线y= x3+
x3+ ,求曲线过点P(2,4)的切线方程;
,求曲线过点P(2,4)的切线方程;
 x3+
x3+ ,求曲线过点P(2,4)的切线方程;
,求曲线过点P(2,4)的切线方程;4x-y-4=0或x-y+2=0.
设曲线y= x3+
x3+ 与过点P(2,4)的切线相切于点A
与过点P(2,4)的切线相切于点A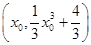 ,
,
则切线的斜率k=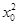 ,切线方程为y-
,切线方程为y-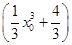 =
=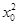 (x-x0),即y=
(x-x0),即y=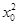 x-
x-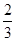
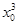 +
+ .
.
因为点P(2,4)在切线上,
所以4=2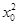 -
-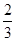
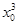 +
+ ,即
,即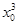 -3
-3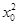 +4=0,
+4=0,
解得x0=-1或x0=2,
故所求的切线方程为4x-y-4=0或x-y+2=0.
 x3+
x3+ 与过点P(2,4)的切线相切于点A
与过点P(2,4)的切线相切于点A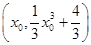 ,
,则切线的斜率k=
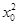 ,切线方程为y-
,切线方程为y-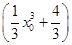 =
=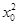 (x-x0),即y=
(x-x0),即y=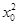 x-
x-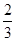
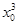 +
+ .
.因为点P(2,4)在切线上,
所以4=2
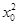 -
-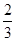
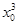 +
+ ,即
,即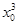 -3
-3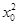 +4=0,
+4=0,解得x0=-1或x0=2,
故所求的切线方程为4x-y-4=0或x-y+2=0.

练习册系列答案
相关题目
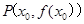 是函数
是函数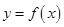 图像上一点,曲线
图像上一点,曲线 处的切线交
处的切线交 轴于点
轴于点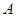 ,
,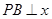 轴,垂足为
轴,垂足为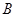 . 若
. 若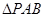 的面积为
的面积为 ,则
,则 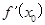 与
与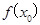 满足关系式( )
满足关系式( )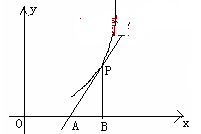
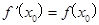
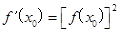
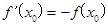
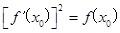
 与曲线
与曲线 切于点
切于点 ,则
,则 的值为__________.
的值为__________.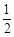 ,
,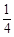 )的切线的倾斜角是( )
)的切线的倾斜角是( )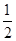 x-cosx在x=
x-cosx在x=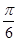 处的切线方程为________.
处的切线方程为________.