题目内容
16.若向量$\overrightarrow a,\overrightarrow b$满足:$|\overrightarrow a|=1$,$(\overrightarrow a+\overrightarrow b)⊥\overrightarrow a$,$(2\overrightarrow a+\overrightarrow b)⊥\overrightarrow b$,则$|\overrightarrow b|$=( )| A. | 2 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 由已知两个垂直,得到数量积为0,整理得到所求.
解答 解:因为$(\overrightarrow a+\overrightarrow b)⊥\overrightarrow a$,$(2\overrightarrow a+\overrightarrow b)⊥\overrightarrow b$,
所以$(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}$=0,$(2\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{b}$=0,
所以$\overrightarrow{a}•\overrightarrow{b}=-{\overrightarrow{a}}^{2}=-\frac{1}{2}{\overrightarrow{b}}^{2}$,所以${\overrightarrow{b}}^{2}$=2,
所以$|\overrightarrow{b}|=\sqrt{2}$;
故选:B.
点评 本题考查了向量垂直,数量积为0,属于基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
6.在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列结论错误的是( )
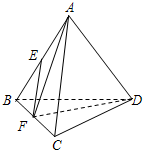

| A. | 异面直线AB与CD所成的角为90° | B. | 直线AB与平面BCD成的角为60° | ||
| C. | 直线EF∥平面ACD | D. | 平面AFD垂直平面BCD |
7.已知$tan(α+\frac{π}{5})=2$,$tan(β-\frac{4π}{5})=-3$,则tan(α-β)=( )
| A. | 1 | B. | -$\frac{5}{7}$ | C. | $\frac{5}{7}$ | D. | -1 |
11.已知数列{an}的通项公式是an=$\frac{n+2}{n+1}$,则这个数列是( )
| A. | 递增数列 | B. | 递减数列 | C. | 常数列 | D. | 摆动数列 |
5.已知定义在实数集R的函数f(x)满足f(1)=4,且f(x)导函数f′(x)<3,则不等式f(lnx)>3lnx+1的解集为( )
| A. | (1,+∞) | B. | (e,+∞) | C. | (0,1) | D. | (0,e) |