题目内容
13.设A(x1,y1),B(x2,y2)是函数f(x)=$\frac{1}{2}+{log_2}\frac{x}{1-x}$的图象上任意两点,P是AB中点,且P的横坐标为$\frac{1}{2}$.(Ⅰ)求证:P点的纵坐标为定值;
(Ⅱ)若Sn=$f(\frac{1}{n})+f(\frac{2}{n})+…+f(\frac{n-1}{n})$,n∈N*,且n≥2,求Sn.
分析 (Ⅰ)通过中点坐标公式及已知条件,可得x1=1-x2或x2=1-x1,利用对数的运算性质可得结论;
(Ⅱ)通过Sn中前后对应位置的两项相加即得结论.
解答 (Ⅰ)证明:设P点的坐标为(x,y),
∵P是AB的中点,
∴$\frac{1}{2}$(x1+x2)=x=$\frac{1}{2}$,得x1+x2=1,
则x1=1-x2或x2=1-x1,
∴y=$\frac{1}{2}$(y1+y2)
=$\frac{1}{2}$[f(x1)+f(x2)]
=$\frac{1}{2}$($\frac{1}{2}$+log2$\frac{{x}_{1}}{1-{x}_{1}}$+$\frac{1}{2}$+$lo{g}_{2}\frac{{x}_{2}}{1-{x}_{2}}$)
=$\frac{1}{2}$(1+log2$\frac{{x}_{1}}{1-{x}_{1}}$+$\frac{1}{2}$+$lo{g}_{2}\frac{{x}_{2}}{1-{x}_{2}}$)
=$\frac{1}{2}$(1+log2$\frac{{x}_{1}}{1-{x}_{1}}$•$\frac{{x}_{2}}{1-{x}_{2}}$)
=$\frac{1}{2}$(1+log2$\frac{{x}_{1}•{x}_{2}}{{x}_{1}•{x}_{2}}$)
=$\frac{1}{2}$,
∴P点的纵坐标为定值$\frac{1}{2}$;
(Ⅱ)解:由(Ⅰ)知x1+x2=1,f(x1)+f(x2)=y1+y2=1,
又∵Sn=$f(\frac{1}{n})+f(\frac{2}{n})+…+f(\frac{n-1}{n})$,
∴Sn=f($\frac{n-1}{n}$)+…+f($\frac{1}{n}$),
两式相加,得2Sn=[f($\frac{1}{n}$)+f($\frac{n-1}{n}$)]+…+[f($\frac{n-1}{n}$)+f($\frac{1}{n}$)]
=$\underbrace{1+1+…+1}_{n-1}$=n-1,
∴Sn=$\frac{n-1}{2}$(n≥2,n∈N*).
点评 本题考查数列的求和,涉及到中点坐标公式、对数的运算性质等知识,利用并项法是解决本题的关键,注意解题方法的积累,属于中档题.

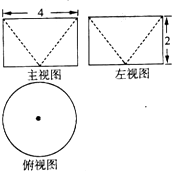 已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为V1.直径为6的球的体积为V2,则V1:V2=( )
已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为V1.直径为6的球的体积为V2,则V1:V2=( )| A. | 1:2 | B. | 2:27 | C. | 1:3 | D. | 4:27 |
且只有两个年级选择甲博物馆的方案有( )
| A. | A62×A54种 | B. | A62×54种 | C. | C62×A54种 | D. | C62×54 |
| A. | {x|x<-5或x>-2} | B. | {x|x≤-5或x≥-2} | C. | {x|x≤-3或x≥-1} | D. | {x|x<-3或x>-1} |
 如图,网格纸是由边长为x的小正方形组成,某几何体的三视图如图中粗线所示,已知该几何体的体积为128,则x=( )
如图,网格纸是由边长为x的小正方形组成,某几何体的三视图如图中粗线所示,已知该几何体的体积为128,则x=( )| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{3}{2}$ |
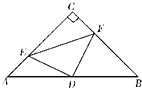 如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①四边形CEDF有可能成为正方形;②△DFE是等腰直角三角形;③四边形CEDF的面积是定值;④点C到线段EF的最大距离为$\sqrt{2}$.
如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①四边形CEDF有可能成为正方形;②△DFE是等腰直角三角形;③四边形CEDF的面积是定值;④点C到线段EF的最大距离为$\sqrt{2}$.