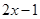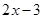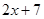题目内容
已知函数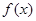 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件:
①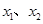 、
、 是定义域中的数时,有
是定义域中的数时,有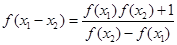 ;
;
②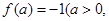
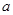 是定义域中的一个数);
是定义域中的一个数);
③当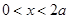 时,
时,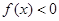 .
.
(1)判断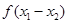 与
与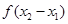 之间的关系,并推断函数
之间的关系,并推断函数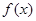 的奇偶性;
的奇偶性;
(2)判断函数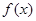 在
在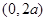 上的单调性,并证明;
上的单调性,并证明;
(3)当函数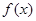 的定义域为
的定义域为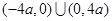 时,
时,
①求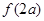 的值;②求不等式
的值;②求不等式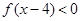 的解集.
的解集.
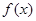 的定义域关于原点对称,且满足以下三个条件:
的定义域关于原点对称,且满足以下三个条件:①
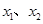 、
、 是定义域中的数时,有
是定义域中的数时,有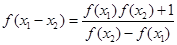 ;
;②
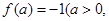
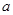 是定义域中的一个数);
是定义域中的一个数);③当
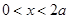 时,
时,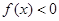 .
.(1)判断
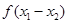 与
与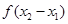 之间的关系,并推断函数
之间的关系,并推断函数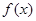 的奇偶性;
的奇偶性;(2)判断函数
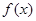 在
在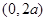 上的单调性,并证明;
上的单调性,并证明;(3)当函数
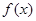 的定义域为
的定义域为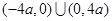 时,
时,①求
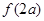 的值;②求不等式
的值;②求不等式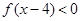 的解集.
的解集. (1)略
(2)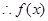 在
在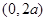 上是增函数;
上是增函数;
(3)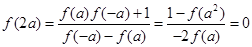 ,不等式的解集是
,不等式的解集是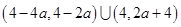 .
.
(2)
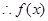 在
在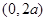 上是增函数;
上是增函数;(3)
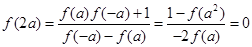 ,不等式的解集是
,不等式的解集是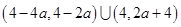 .
.(1)不妨令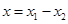 ,则
,则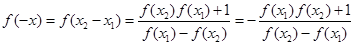
 ,
,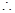
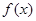 是奇函数;
是奇函数;
(2)在 上任取两个实数
上任取两个实数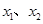 ,且
,且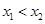 ,则有
,则有 ,然后再根据x1和x2的范围,分别讨论差值符号,进行证明出f(x)单调性.
,然后再根据x1和x2的范围,分别讨论差值符号,进行证明出f(x)单调性.
(3)先根据条件得 ,所以
,所以
 ,然后再利用f(x)的单调性去掉法则符合f转化为关于x的一次不等式即可.
,然后再利用f(x)的单调性去掉法则符合f转化为关于x的一次不等式即可.
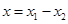 ,则
,则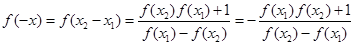
 ,
,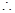
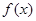 是奇函数;
是奇函数;(2)在
 上任取两个实数
上任取两个实数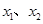 ,且
,且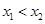 ,则有
,则有 ,然后再根据x1和x2的范围,分别讨论差值符号,进行证明出f(x)单调性.
,然后再根据x1和x2的范围,分别讨论差值符号,进行证明出f(x)单调性.(3)先根据条件得
 ,所以
,所以 ,然后再利用f(x)的单调性去掉法则符合f转化为关于x的一次不等式即可.
,然后再利用f(x)的单调性去掉法则符合f转化为关于x的一次不等式即可.
练习册系列答案
相关题目
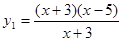 ,
,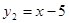 ; (2)
; (2) 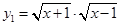 ,
,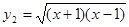
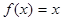 ,
,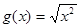 ; (4)
; (4)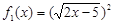 ,
,
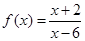 ,
,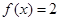 时,求
时,求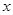 的值;
的值;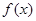 在
在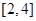 上是减函数,并求函数的最大值和最小值.
上是减函数,并求函数的最大值和最小值.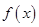 与
与 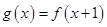 B.
B. 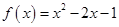 与
与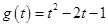
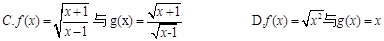
 上是减函数,则实数a的取值范围是( )
上是减函数,则实数a的取值范围是( ) -
- ,+∞) B (-∞,-
,+∞) B (-∞,-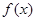 是
是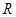 上最小正周期为2的周期函数,且当
上最小正周期为2的周期函数,且当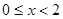 时,
时, ,则函数
,则函数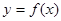 的图象在区间
的图象在区间 上与
上与 轴的交点的个数为 .
轴的交点的个数为 .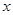 表示P点的行程,
表示P点的行程,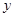 表示PA的长,求
表示PA的长,求 。
。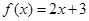 ,
,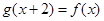 ,则函数
,则函数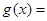 ( )
( )