题目内容
(本小题满分14分)已知各项均不为零的数列{an}的前n项和为Sn,且满足a1=c,
2Sn=an an+1+r.
(1)若r=-6,数列{an}能否成为等差数列?若能,求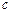 满足的条件;若不能,请说明理由;
满足的条件;若不能,请说明理由;
(2)设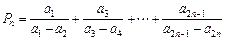 ,
,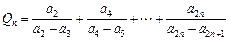 ,
,
若r>c>4,求证:对于一切n∈N*,不等式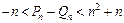 恒成立.
恒成立.
2Sn=an an+1+r.
(1)若r=-6,数列{an}能否成为等差数列?若能,求
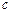 满足的条件;若不能,请说明理由;
满足的条件;若不能,请说明理由;(2)设
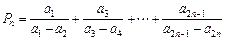 ,
,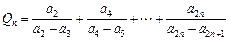 ,
,若r>c>4,求证:对于一切n∈N*,不等式
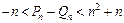 恒成立.
恒成立.解:(1)n=1时,2a1=a1 a2+r,∵a1=c≠0,∴2c=ca2+r,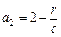 .
.
n≥2时,2Sn=an an+1+r,① 2Sn-1=an-1 an+r,②
①-②,得2an=an(an+1-an-1).∵an≠0,∴an+1-an-1=2.
则a1,a3,a5,…,a2n-1,… 成公差为2的等差数列,a2n-1=a1+2(n-1).
a2,a4,a6,…,a2n,… 成公差为2的等差数列, a2n=a2+2(n-1).
要使{an}为等差数列,当且仅当a2-a1=1.即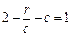 .r=c-c2.
.r=c-c2.
∵r=-6,∴c2-c-6=0,c=-2或3.
∵当c=-2,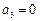 ,不合题意,舍去.
,不合题意,舍去.
∴当且仅当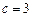 时,数列
时,数列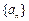 为等差数列 ……………………………………6分
为等差数列 ……………………………………6分
(2)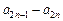 =[a1+2(n-1)]-[a2+2(n-1)]=a1-a2=
=[a1+2(n-1)]-[a2+2(n-1)]=a1-a2=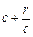 -2.
-2.
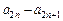 =[a2+2(n-1)]-(a1+2n)=a2-a1-2=-(
=[a2+2(n-1)]-(a1+2n)=a2-a1-2=-(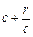 ). ………………………8分
). ………………………8分
∴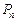
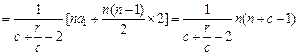
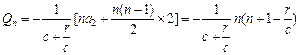 .
.
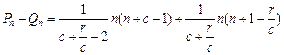
=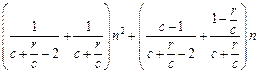 . ……………………………………10分
. ……………………………………10分
∵r>c>4,∴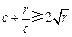 >4,∴
>4,∴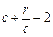 >2.∴0<
>2.∴0<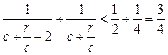 <1.
<1.
又∵r>c>4,∴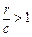 ,则0<
,则0<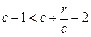 ;
;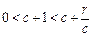 .
.
∴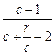 <1.
<1.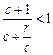 .∴
.∴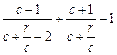 <1.
<1.
所以: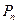
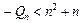
又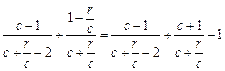 >-1.
>-1.
所以: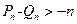
综上,对于一切n∈N*,不等式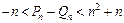 恒成立. …………………14分
恒成立. …………………14分
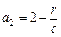 .
.n≥2时,2Sn=an an+1+r,① 2Sn-1=an-1 an+r,②
①-②,得2an=an(an+1-an-1).∵an≠0,∴an+1-an-1=2.
则a1,a3,a5,…,a2n-1,… 成公差为2的等差数列,a2n-1=a1+2(n-1).
a2,a4,a6,…,a2n,… 成公差为2的等差数列, a2n=a2+2(n-1).
要使{an}为等差数列,当且仅当a2-a1=1.即
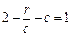 .r=c-c2.
.r=c-c2. ∵r=-6,∴c2-c-6=0,c=-2或3.
∵当c=-2,
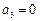 ,不合题意,舍去.
,不合题意,舍去.∴当且仅当
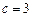 时,数列
时,数列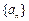 为等差数列 ……………………………………6分
为等差数列 ……………………………………6分(2)
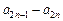 =[a1+2(n-1)]-[a2+2(n-1)]=a1-a2=
=[a1+2(n-1)]-[a2+2(n-1)]=a1-a2=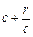 -2.
-2.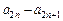 =[a2+2(n-1)]-(a1+2n)=a2-a1-2=-(
=[a2+2(n-1)]-(a1+2n)=a2-a1-2=-(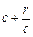 ). ………………………8分
). ………………………8分∴
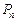
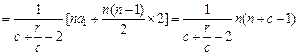
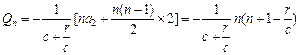 .
. 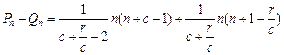
=
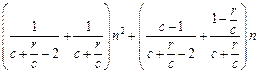 . ……………………………………10分
. ……………………………………10分∵r>c>4,∴
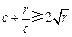 >4,∴
>4,∴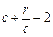 >2.∴0<
>2.∴0<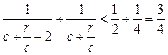 <1.
<1.又∵r>c>4,∴
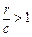 ,则0<
,则0<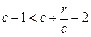 ;
;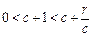 .
.∴
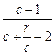 <1.
<1.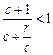 .∴
.∴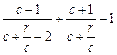 <1.
<1.所以:
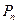
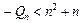
又
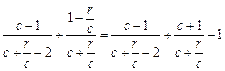 >-1.
>-1. 所以:
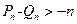
综上,对于一切n∈N*,不等式
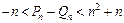 恒成立. …………………14分
恒成立. …………………14分略

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
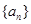 满足
满足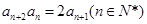 ,且
,且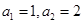 ,则数列
,则数列 项的乘积为
项的乘积为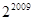
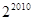
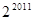
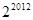
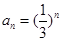 ,把数列
,把数列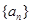 的各项同排成如下的三角形:记
的各项同排成如下的三角形:记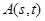 表示第s行的第t个数,则A(11,12)= ( )
表示第s行的第t个数,则A(11,12)= ( )




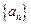 满足
满足 +
+ =4n-3(n∈
=4n-3(n∈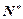 ).
). =2,求数列
=2,求数列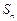 ;
;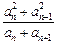 ≥5成立,求
≥5成立,求 为偶数时,
为偶数时, 的前n项和为
的前n项和为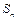 ,且
,且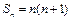 (
(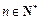 ).
).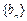 满足:
满足: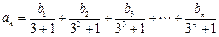 ,求数列
,求数列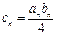 (
(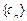 的前n项和
的前n项和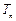 .
. 中,已知
中,已知 ,
, ,
, ,…,
,…, ,则
,则 的最大值为______________.
的最大值为______________. )第2个数是__________.
)第2个数是__________.
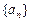 的前
的前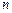 项和为
项和为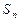 ,且
,且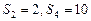 ,则
,则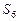 等于( )
等于( )