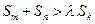题目内容
本小题满分12分)
已知数列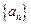 满足
满足 +
+ =4n-3(n∈
=4n-3(n∈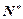 ).
).
(I)若 =2,求数列
=2,求数列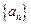 的前n项和
的前n项和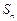 ;
;
(II)若对任意n∈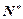 ,都有
,都有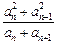 ≥5成立,求
≥5成立,求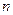 为偶数时,
为偶数时, 的取值范围.
的取值范围.
已知数列
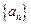 满足
满足 +
+ =4n-3(n∈
=4n-3(n∈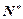 ).
).(I)若
 =2,求数列
=2,求数列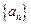 的前n项和
的前n项和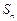 ;
;(II)若对任意n∈
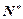 ,都有
,都有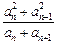 ≥5成立,求
≥5成立,求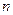 为偶数时,
为偶数时, 的取值范围.
的取值范围.解:(I)由 +
+ =4n-3(n∈
=4n-3(n∈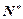 )得
)得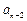 +
+ =4n+1(n∈
=4n+1(n∈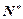 ).
).
两式相减,得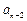 -
- =4.
=4.
所以数列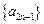 是首项为
是首项为 ,公差为4的等差数列;数列
,公差为4的等差数列;数列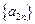 是首项为
是首项为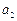 ,公差为4的等差数列. …………………………. ………………………………………………2分
,公差为4的等差数列. …………………………. ………………………………………………2分
由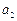 +
+ =1,
=1, =2,得
=2,得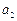 =-1.
=-1.
所以 =
=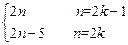 (k∈Z).…………………………………………………3分
(k∈Z).…………………………………………………3分
①当n为奇数时, =2n,
=2n, =2n-3,
=2n-3,
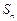 =
= +
+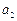 +
+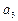 +…+
+…+ =(
=( +
+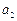 )+(
)+(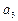 +
+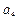 )+…+(
)+…+(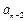 +
+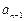 )+
)+
=1+9+…+(4n-11)+2n=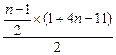 +2n=
+2n= .
.
……. ………………………………………………5分
②当n为偶数时,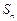 =
= +
+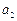 +
+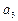 +…+
+…+ =(
=( +
+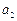 )+(
)+(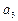 +
+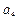 )+…+(
)+…+(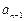 +
+ )
)
=1+9+…+(4n-7) = .
.
所以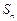 =
=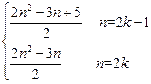 (k∈Z)……………………………………7分
(k∈Z)……………………………………7分
(II)由(I)知, =
=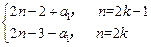 (k∈Z)
(k∈Z)
当n为偶数时, =2n-3-
=2n-3- ,
, =2n+
=2n+
由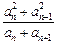 ≥5,得
≥5,得 +
+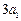 ≥
≥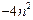 +16n-12. ………………………………….9分
+16n-12. ………………………………….9分
令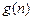 =
=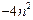 +16n-12=
+16n-12=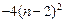 +4
+4
当n=2时,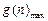 =4,所以
=4,所以 +
+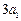 ≥4
≥4
解得 ≥1或
≥1或 ≤-4……………………………………………………11分
≤-4……………………………………………………11分
综上所述, 的取值范围是
的取值范围是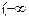 ,
,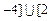 ,
,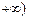 .……………………………………12分
.……………………………………12分
 +
+ =4n-3(n∈
=4n-3(n∈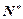 )得
)得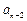 +
+ =4n+1(n∈
=4n+1(n∈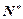 ).
).两式相减,得
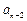 -
- =4.
=4. 所以数列
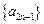 是首项为
是首项为 ,公差为4的等差数列;数列
,公差为4的等差数列;数列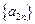 是首项为
是首项为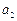 ,公差为4的等差数列. …………………………. ………………………………………………2分
,公差为4的等差数列. …………………………. ………………………………………………2分由
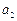 +
+ =1,
=1, =2,得
=2,得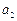 =-1.
=-1.所以
 =
=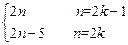 (k∈Z).…………………………………………………3分
(k∈Z).…………………………………………………3分①当n为奇数时,
 =2n,
=2n, =2n-3,
=2n-3,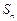 =
= +
+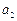 +
+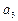 +…+
+…+ =(
=( +
+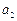 )+(
)+(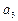 +
+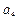 )+…+(
)+…+(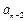 +
+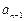 )+
)+
=1+9+…+(4n-11)+2n=
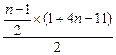 +2n=
+2n= .
.……. ………………………………………………5分
②当n为偶数时,
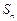 =
= +
+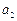 +
+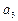 +…+
+…+ =(
=( +
+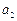 )+(
)+(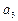 +
+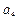 )+…+(
)+…+(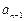 +
+ )
)=1+9+…+(4n-7) =
 .
.所以
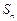 =
=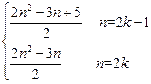 (k∈Z)……………………………………7分
(k∈Z)……………………………………7分(II)由(I)知,
 =
=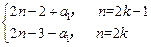 (k∈Z)
(k∈Z)当n为偶数时,
 =2n-3-
=2n-3- ,
, =2n+
=2n+
由
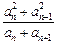 ≥5,得
≥5,得 +
+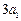 ≥
≥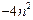 +16n-12. ………………………………….9分
+16n-12. ………………………………….9分令
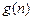 =
=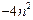 +16n-12=
+16n-12=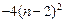 +4
+4当n=2时,
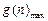 =4,所以
=4,所以 +
+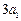 ≥4
≥4解得
 ≥1或
≥1或 ≤-4……………………………………………………11分
≤-4……………………………………………………11分综上所述,
 的取值范围是
的取值范围是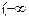 ,
,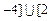 ,
,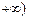 .……………………………………12分
.……………………………………12分略

练习册系列答案
相关题目
 和
和 的通项公式分别为
的通项公式分别为 ,
, (
( ),将集合
),将集合 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列 。
。 中有多少项不是数列
中有多少项不是数列 的前
的前 项和
项和 (
(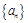 满足
满足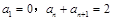 ,则
,则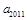 的值为 ( )
的值为 ( )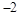
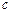 满足的条件;若不能,请说明理由;
满足的条件;若不能,请说明理由;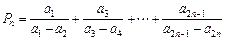 ,
,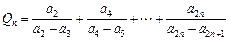 ,
,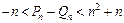 恒成立.
恒成立.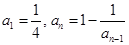 ,则
,则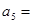 ( )
( )
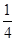
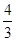
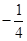
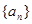 的前n项的和
的前n项的和 ,那么这个数列的通项公式为( )
,那么这个数列的通项公式为( )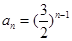
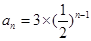
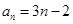
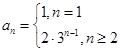
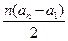 .
.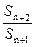 +
+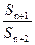 ,求数列﹛bn﹜的前n项和Tn;
,求数列﹛bn﹜的前n项和Tn;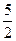 ,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。
,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。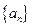 的前
的前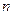 项和为
项和为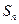 ,若
,若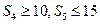 ,则
,则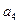 的最大值为__________.
的最大值为__________.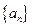 的前
的前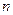 项和为
项和为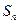 ,且满足:
,且满足: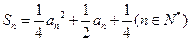
 )求
)求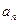 ;
; ,求数列
,求数列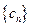 的前
的前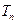 ;
;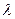 为实数,对满足
为实数,对满足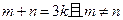 的任意正整数
的任意正整数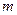 、
、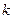 ,不等式
,不等式