题目内容
设数列{an}满足a1 = 3,an+1 = 2an+n·2n+1+3n,n≥1。
(1)求数列{an}的通项公式;
(2)求数列{an}的前n项之和Sn。
(1)求数列{an}的通项公式;
(2)求数列{an}的前n项之和Sn。
(1)an=2n-1·(n2-n)+3n;
(2)Sn= - (n-2)·2n+1+(n-1)·n·2n-4= - (n-2)·2n+1+(n-1)·n·2n-4
(2)Sn= - (n-2)·2n+1+(n-1)·n·2n-4= - (n-2)·2n+1+(n-1)·n·2n-4
(1) an= 2an-1+(n-1)·2n+3n-1
=2[2an-2+(n-2)·2n-1+3n-2]+(n-1)·2n+3n-1
=22an-2+[(n-2)+(n-1)]·2n+(2·3n-2+3n-1)
=22[2an-3+(n-3)·2n-2+3n-3]+[(n-2)+(n-1)]·2n+(2·3n-2+3n-1)
=23an-3+[(n-3)+(n-2)+(n-1)]·2n+(22·3n-3+2·3n-2+3n-1)
=……
=2 n-1a1+[1+2+3+…+(n-1)]·2n+(2n-2·3+2n-3·32+…+3n-1)
=2n-1·3+·2n+2n-2·3·
=2n-1·(n2-n+3)+2n-1·3[()n-1-1]
=2n-1·(n2-n)+3n。
(2)设数列{bn},其中bn =2n-1·(n2-n),Mn 为其前n项和,则Sn= Mn+3n。
Mn =0+1·2·21+2·3·22+3·4·23+…+(n-1)·n·2n-1,
2Mn = 1·2·22+2·3·23+…+(n-1)·n·2n,
相减得 - Mn = 1·2·2+2·2·22+3·2·23+…+2·(n-1)·2n-1- (n-1)n·2n
=1·22+2·23+3·24+…+(n-1)·2n- (n-1)n·2n,
-2 Mn = 1·23+2·24+3·25+…+(n-1)·2n+1- (n-1)·n·2n+1,
相减得 Mn = 1·22+23+24+…+2n- (n-1)·2 n+1+(n-1)n·2n
= (2-n)·2 n+1+(n-1)·n·2n-4,
Sn = Mn+3+32+…+3n
= - (n-2)·2n+1+(n-1)·n·2n-4。
=2[2an-2+(n-2)·2n-1+3n-2]+(n-1)·2n+3n-1
=22an-2+[(n-2)+(n-1)]·2n+(2·3n-2+3n-1)
=22[2an-3+(n-3)·2n-2+3n-3]+[(n-2)+(n-1)]·2n+(2·3n-2+3n-1)
=23an-3+[(n-3)+(n-2)+(n-1)]·2n+(22·3n-3+2·3n-2+3n-1)
=……
=2 n-1a1+[1+2+3+…+(n-1)]·2n+(2n-2·3+2n-3·32+…+3n-1)
=2n-1·3+·2n+2n-2·3·
=2n-1·(n2-n+3)+2n-1·3[()n-1-1]
=2n-1·(n2-n)+3n。
(2)设数列{bn},其中bn =2n-1·(n2-n),Mn 为其前n项和,则Sn= Mn+3n。
Mn =0+1·2·21+2·3·22+3·4·23+…+(n-1)·n·2n-1,
2Mn = 1·2·22+2·3·23+…+(n-1)·n·2n,
相减得 - Mn = 1·2·2+2·2·22+3·2·23+…+2·(n-1)·2n-1- (n-1)n·2n
=1·22+2·23+3·24+…+(n-1)·2n- (n-1)n·2n,
-2 Mn = 1·23+2·24+3·25+…+(n-1)·2n+1- (n-1)·n·2n+1,
相减得 Mn = 1·22+23+24+…+2n- (n-1)·2 n+1+(n-1)n·2n
= (2-n)·2 n+1+(n-1)·n·2n-4,
Sn = Mn+3+32+…+3n
= - (n-2)·2n+1+(n-1)·n·2n-4。

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 和
和 的通项公式分别为
的通项公式分别为 ,
, (
( ),将集合
),将集合 中的元素从小到大依次排列,构成数列
中的元素从小到大依次排列,构成数列 。
。 中有多少项不是数列
中有多少项不是数列 的前
的前 项和
项和 (
(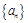 满足
满足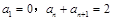 ,则
,则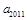 的值为 ( )
的值为 ( )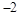
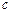 满足的条件;若不能,请说明理由;
满足的条件;若不能,请说明理由;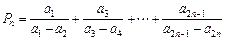 ,
,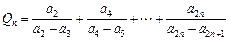 ,
,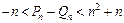 恒成立.
恒成立. 中,
中,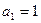 ,
, ,则前6项和为_________
,则前6项和为_________ )求数列
)求数列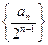 的前n项和.
的前n项和.
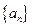 的前
的前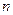 项和为
项和为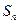 ,且满足:
,且满足: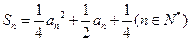
 )求
)求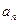 ;
; ,求数列
,求数列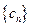 的前
的前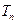 ;
;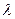 为实数,对满足
为实数,对满足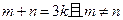 的任意正整数
的任意正整数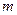 、
、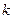 ,不等式
,不等式