题目内容
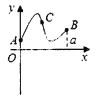
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<![]() )的图象如图所示.
)的图象如图所示.
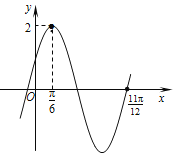
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调增区间;
(3)若x∈[-![]() ,0],求函数f(x)的值域.
,0],求函数f(x)的值域.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式;
(2)令2kπ![]() 2x
2x![]() 2kπ
2kπ![]() ,k∈z,求得x的范围,可得函数的增区间;
,k∈z,求得x的范围,可得函数的增区间;
(3)由x∈[![]() ,0],利用正弦函数的定义域和值域求得f(x)的值域.
,0],利用正弦函数的定义域和值域求得f(x)的值域.
解:(1)由函数的图象可得A=2,![]() T=
T=![]()
![]() =
=![]() -
-![]() ,求得ω=2.
,求得ω=2.
再根据五点法作图可得2×![]() +φ=
+φ=![]() ,∴φ=
,∴φ=![]() ,故f(x)=2sin(2x+
,故f(x)=2sin(2x+![]() ).
).
(2)令2kπ-![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]() ,k∈z,求得kπ-
,k∈z,求得kπ-![]() ≤x≤kπ+
≤x≤kπ+![]() ,
,
故函数的增区间为[kπ-![]() ,kπ+
,kπ+![]() ],k∈z.
],k∈z.
(3)若x∈[-![]() ,0],则2x+
,0],则2x+![]() ∈[-
∈[-![]() ,
,![]() ],∴sin(2x+
],∴sin(2x+![]() )∈[-1,
)∈[-1,![]() ],
],
故f(x)∈[-2,1].

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案【题目】为提升教师专业功底,引领青年教师成长,某市教育局举行了全市“园丁杯”课堂教学比赛,在这次比赛中,通过采用录像课评比的片区预赛,有![]() 共10位选手脱颖而出进入全市决赛.决赛采用现场上课形式,从学科评委库中采用随机抽样抽选代号1,2,3,…,7的7名评委,规则是:选手上完课,评委们当初评分,并从7位评委评分中去掉一个最高分,去掉一个最低分,根据剩余5位评委的评分,算出平均分作为该选手的最终得分.记评委
共10位选手脱颖而出进入全市决赛.决赛采用现场上课形式,从学科评委库中采用随机抽样抽选代号1,2,3,…,7的7名评委,规则是:选手上完课,评委们当初评分,并从7位评委评分中去掉一个最高分,去掉一个最低分,根据剩余5位评委的评分,算出平均分作为该选手的最终得分.记评委![]() 对某选手评分排名与该选手最终排名的差的绝对值为“评委
对某选手评分排名与该选手最终排名的差的绝对值为“评委![]() 对这位选手的分数排名偏差”
对这位选手的分数排名偏差”![]() .排名规则:由高到低依次排名,如果选手分数一样,认定名次并列(如:选手
.排名规则:由高到低依次排名,如果选手分数一样,认定名次并列(如:选手![]() 分数一致排在第二,则认为他们同属第二名,没有第三名,接下来分数为第四名).七位评委评分情况如下表所示:
分数一致排在第二,则认为他们同属第二名,没有第三名,接下来分数为第四名).七位评委评分情况如下表所示:
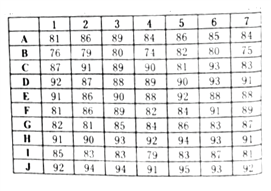
(1)根据最终评分表,填充如下表格:

(2)试借助评委评分分析表,根据评委对各选手的排名偏差的平方和,判断评委4与评委5在这次活动中谁评判更准确.
____号评委评分分析表
选手 | A | B | C | D | E | F | G | H | I | J |
最终排名 | ||||||||||
评分排名 | ||||||||||
排名偏差 |
(3)从这10位选手中任意选出3位,记其中评委4比评委5对选手排名偏差小的选手数位![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.