Question

【题目】已知偶函数的定义域为，值域为．

（1）求实数的值；

（2）若，求实数的值；

（3）若,求的值．

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）根据函数为偶函数，，构造关于的方程组，可得的值；

（2）由（1）中函数的解析式，分别令和，解得，结合题中所给的集合E，可求得的可取值；

（3）求出函数的导函数，判断函数的单调性，进而根据函数的值域为，，分和两种情况讨论，构造关于的方程组，进而得到的值.

（1）因为函数为偶函数，

所以，即，

所以，因为为非零实数，

所以，即；

(2)令f（a）=0，即，a=±1，取a=﹣1；

令f（a）=，即，a=±2，取a=﹣2，

故a=﹣1或﹣2．

（3）∵是偶函数，且，

则函数f（x）在（﹣∞，0）上是减函数，在（0，+∞）上是增函数．

∵x≠0，∴由题意可知：或．

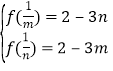若，则有，即，

整理得，此时方程组无负解；

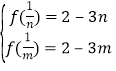若，则有，即，

∴m，n为方程x2﹣3x+1=0，的两个根．∵，∴m＞n＞0，

∴