题目内容
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2.

(1)证明PA∥平面BDE;
(2)证明AC⊥平面PBD;

(1)证明PA∥平面BDE;
(2)证明AC⊥平面PBD;
解:(1)证明:设AC∩BD=H,
连结EH.在△ADC中,因为AD=CD,且DB平分∠ADC,所以H为AC
的中点.
又由题设,E为PC的中点,故EH∥PA.又EH?平面BDE且PA ?平面BDE,
所以PA∥平面BDE.
(2)证明:因为PD⊥平面ABCD,AC?平面ABCD,所以PD⊥AC.
由(1)可得,DB⊥AC.又PD∩DB=D,故AC⊥平面PBD.
连结EH.在△ADC中,因为AD=CD,且DB平分∠ADC,所以H为AC
的中点.
又由题设,E为PC的中点,故EH∥PA.又EH?平面BDE且PA ?平面BDE,
所以PA∥平面BDE.
(2)证明:因为PD⊥平面ABCD,AC?平面ABCD,所以PD⊥AC.
由(1)可得,DB⊥AC.又PD∩DB=D,故AC⊥平面PBD.
略

练习册系列答案
相关题目
 与正三角形
与正三角形 组合而成的平面图形中,
组合而成的平面图形中, 现将正三角形
现将正三角形 折成四棱锥
折成四棱锥 ,使
,使 在平面
在平面 上.
上.

 ⊥平面
⊥平面 ;
; 与平面
与平面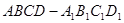 的侧面
的侧面 内有一动点
内有一动点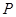 到直线
到直线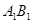 与直线
与直线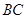 的距离相等,则动点
的距离相等,则动点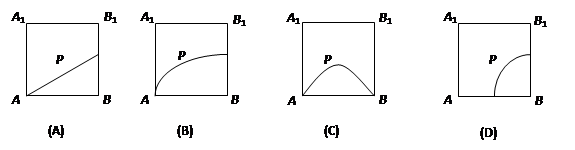
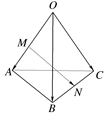
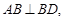 沿BD将
沿BD将 折起,使面
折起,使面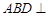 面
面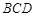 ,连结AC,则在四面体ABCD的四个面中,互相垂直的平面共有( )对
,连结AC,则在四面体ABCD的四个面中,互相垂直的平面共有( )对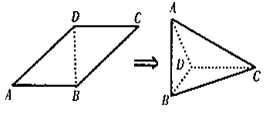
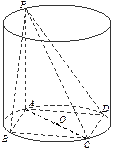
 内接于圆柱下底面的圆
内接于圆柱下底面的圆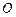 ,
,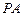 是圆柱的母线,若
是圆柱的母线,若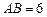 ,
,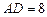 ,此圆柱的体积为
,此圆柱的体积为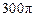 ,求异面直线
,求异面直线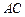 与
与 所成角的余弦值.
所成角的余弦值.
 b+c
b+c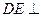 平面ABCD,
平面ABCD,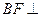 平面ABCD,且FB=2DE=2。
平面ABCD,且FB=2DE=2。
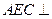 平面AFC。
平面AFC。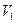 和
和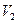 ,则
,则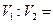 ( )
( )