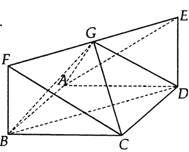
题目内容
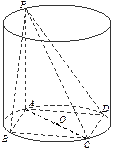
已知矩形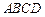 内接于圆柱下底面的圆
内接于圆柱下底面的圆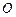 ,
, 是圆柱的母线,若
是圆柱的母线,若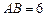 ,
,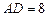 ,此圆柱的体积为
,此圆柱的体积为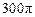 ,求异面直线
,求异面直线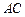 与
与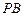 所成角的余弦值.
所成角的余弦值.
 内接于圆柱下底面的圆
内接于圆柱下底面的圆 ,
, 是圆柱的母线,若
是圆柱的母线,若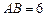 ,
,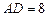 ,此圆柱的体积为
,此圆柱的体积为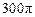 ,求异面直线
,求异面直线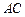 与
与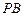 所成角的余弦值.
所成角的余弦值.

解:设圆柱下底面圆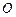 的半径为
的半径为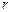 ,连
,连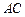 ,
,
由矩形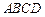 内接于圆
内接于圆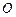 ,可知
,可知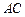 是圆
是圆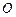 的直径,
的直径,
于是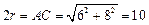 ,得
,得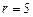 , ……………3分
, ……………3分
又圆柱的体积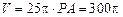 ,可得
,可得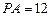 .……6分
.……6分
分别以直线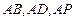 为
为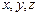 轴,建立空间直角坐标
轴,建立空间直角坐标
系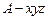 ,可得
,可得 ,………8分
,………8分
设异面直线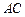 与
与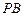 所成角所成的角
所成角所成的角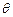 ,向量
,向量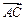 与
与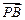 的夹角为
的夹角为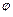 ,
,
则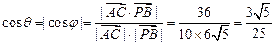 ,
,
故异面直线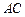 与
与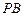 所成角的余弦值为
所成角的余弦值为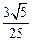 . ………………………………12分
. ………………………………12分
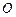 的半径为
的半径为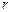 ,连
,连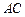 ,
,由矩形
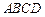 内接于圆
内接于圆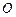 ,可知
,可知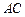 是圆
是圆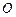 的直径,
的直径,于是
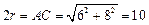 ,得
,得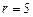 , ……………3分
, ……………3分又圆柱的体积
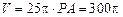 ,可得
,可得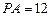 .……6分
.……6分分别以直线
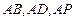 为
为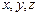 轴,建立空间直角坐标
轴,建立空间直角坐标系
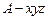 ,可得
,可得 ,………8分
,………8分设异面直线
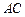 与
与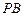 所成角所成的角
所成角所成的角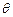 ,向量
,向量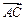 与
与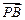 的夹角为
的夹角为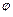 ,
,则
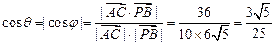 ,
,故异面直线
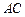 与
与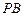 所成角的余弦值为
所成角的余弦值为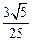 . ………………………………12分
. ………………………………12分 略

练习册系列答案
相关题目
 ABC的边长为1,AE
ABC的边长为1,AE 平面ABC,CD∥AE,且CD=
平面ABC,CD∥AE,且CD=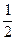 AE.
AE.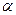 ,AE=
,AE=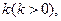 若
若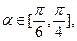 求
求 的取值范围;
的取值范围;
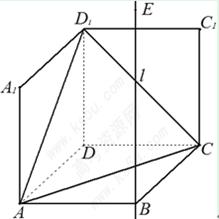
 是
是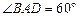 且
且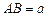 的菱形,
的菱形,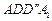 和
和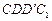 都是正方形。将两个正方形分别沿AD,CD折起,使
都是正方形。将两个正方形分别沿AD,CD折起,使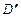 与
与 重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设
重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设 (图2)。
(图2)。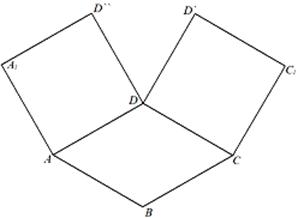
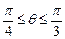 ,求
,求 的取值范围;
的取值范围;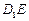 上是否存在点
上是否存在点 ,使平面
,使平面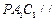 平面
平面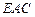 ,若存在,求出
,若存在,求出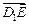 所成的比
所成的比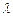 ;若不存在,请说明理由。
;若不存在,请说明理由。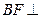 平面ACE。
平面ACE。
 平面BCE;
平面BCE;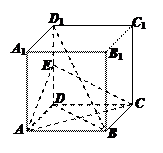 (1)求证:BD1∥平面AEC;
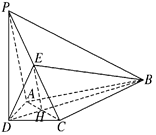
(1)求证:BD1∥平面AEC; 面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=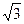 ,设D为
,设D为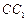 中点,
中点,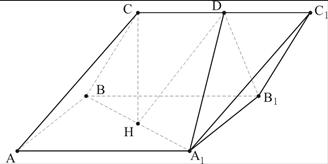
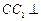 平面
平面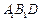 ;
;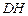 与平面
与平面 所成角的正弦值.
所成角的正弦值.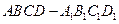 中,底面
中,底面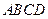 是正方形,侧棱与底面垂直,点
是正方形,侧棱与底面垂直,点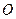 是正方形
是正方形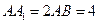 ,点
,点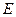 ,
,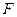 分别在
分别在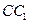 和
和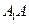 上,且
上,且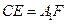 .
.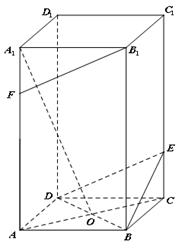
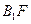 ∥平面
∥平面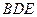 ;
;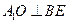 ,求
,求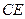 的长;
的长;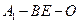 的余弦值.
的余弦值.