题目内容
本小题满分13分)
如图,已知ABCD是边长为2的正方形,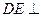 平面ABCD,
平面ABCD,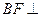 平面ABCD,且FB=2DE=2。
平面ABCD,且FB=2DE=2。

(1)求点E到平面FBC的距离;
(2)求证:平面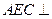 平面AFC。
平面AFC。
如图,已知ABCD是边长为2的正方形,
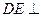 平面ABCD,
平面ABCD,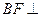 平面ABCD,且FB=2DE=2。
平面ABCD,且FB=2DE=2。
(1)求点E到平面FBC的距离;
(2)求证:平面
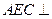 平面AFC。
平面AFC。略
略

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
题目内容
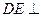 平面ABCD,
平面ABCD,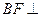 平面ABCD,且FB=2DE=2。
平面ABCD,且FB=2DE=2。
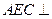 平面AFC。
平面AFC。
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案