题目内容
(本小题满分14分)



 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面

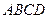 所成的角为45°,底面ABCD为直角梯形,
所成的角为45°,底面ABCD为直角梯形,



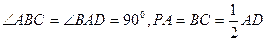
 (Ⅰ)求证:平面
(Ⅰ)求证:平面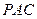 ⊥平面
⊥平面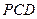 ;(Ⅱ)在棱
;(Ⅱ)在棱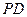 上是否存在一点
上是否存在一点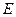 ,使
,使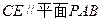 ?若存在,请确定E点的位置;若不存在,请说明理由.
?若存在,请确定E点的位置;若不存在,请说明理由.

|


 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面
|

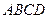 所成的角为45°,底面ABCD为直角梯形,
所成的角为45°,底面ABCD为直角梯形,
|



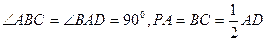
|
|
 (Ⅰ)求证:平面
(Ⅰ)求证:平面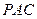 ⊥平面
⊥平面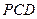 ;(Ⅱ)在棱
;(Ⅱ)在棱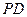 上是否存在一点
上是否存在一点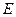 ,使
,使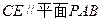 ?若存在,请确定E点的位置;若不存在,请说明理由.
?若存在,请确定E点的位置;若不存在,请说明理由.(Ⅰ) 平面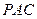 ⊥平面
⊥平面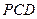
(Ⅱ) E是PD中点,存在E点使得CE//面PAB
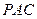 ⊥平面
⊥平面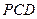
(Ⅱ) E是PD中点,存在E点使得CE//面PAB
解:不妨设PA = 1.
(Ⅰ)由题意PA = BC =" 1," AD = 2.
∵ PA⊥面ABCD,∴ PB与面ABCD所成的角为∠PBA = 45°.………………2分
∴ AB = 1,由∠ABC = ∠BAD = 90°,易得CD = AC = .
由勾股定理逆定理得AC⊥CD.……………………3分
又∵ PA⊥CD, PA∩AC = A,∴ CD⊥面PAC,……………………5分
又CDÌ面PCD,

∴ 面PAC⊥面PCD.……………………7分


 (Ⅱ)分别以AB, AD, AP所在直线分别为x轴, y轴, z轴
(Ⅱ)分别以AB, AD, AP所在直线分别为x轴, y轴, z轴
建立空间直角坐标系. ∴ P(0, 0, 1), C(1, 1, 0), D(0, 2, 0).………… 8分
∴ P(0, 0, 1), C(1, 1, 0), D(0, 2, 0).………… 8分
设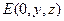 ,则
,则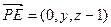 ,
,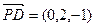 .…………………… 9分
.…………………… 9分
∵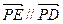 ,∴ y·(-1)-2 (z-1) =" 0" … ①…………………………… 10分
,∴ y·(-1)-2 (z-1) =" 0" … ①…………………………… 10分
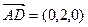 是平面
是平面 的法向量,…………………………… 11分
的法向量,…………………………… 11分
又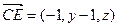 ,由
,由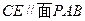 ,∴
,∴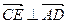 .…………………………… 12分
.…………………………… 12分
∴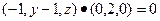 ,∴ y = 1,代入①得z = . …………………13分
,∴ y = 1,代入①得z = . …………………13分
∴ E是PD中点,∴ 存在E点使得CE//面PAB. …………………… 14分
(Ⅰ)由题意PA = BC =" 1," AD = 2.
∵ PA⊥面ABCD,∴ PB与面ABCD所成的角为∠PBA = 45°.………………2分
∴ AB = 1,由∠ABC = ∠BAD = 90°,易得CD = AC = .
由勾股定理逆定理得AC⊥CD.……………………3分
又∵ PA⊥CD, PA∩AC = A,∴ CD⊥面PAC,……………………5分
又CDÌ面PCD,

|
|


 (Ⅱ)分别以AB, AD, AP所在直线分别为x轴, y轴, z轴
(Ⅱ)分别以AB, AD, AP所在直线分别为x轴, y轴, z轴
|
 ∴ P(0, 0, 1), C(1, 1, 0), D(0, 2, 0).………… 8分
∴ P(0, 0, 1), C(1, 1, 0), D(0, 2, 0).………… 8分 |
设
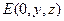 ,则
,则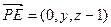 ,
,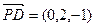 .…………………… 9分
.…………………… 9分∵
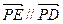 ,∴ y·(-1)-2 (z-1) =" 0" … ①…………………………… 10分
,∴ y·(-1)-2 (z-1) =" 0" … ①…………………………… 10分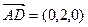 是平面
是平面 的法向量,…………………………… 11分
的法向量,…………………………… 11分又
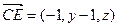 ,由
,由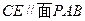 ,∴
,∴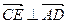 .…………………………… 12分
.…………………………… 12分∴
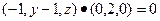 ,∴ y = 1,代入①得z = . …………………13分
,∴ y = 1,代入①得z = . …………………13分∴ E是PD中点,∴ 存在E点使得CE//面PAB. …………………… 14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

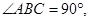
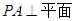 ,
,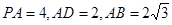 ,BC=6.
,BC=6.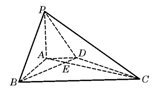
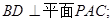
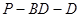 的大小.
的大小. 是直角梯形,
是直角梯形,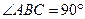 ,
,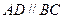 ,
,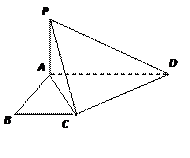
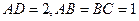 ,
, 平面
平面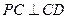 ;
;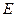 是
是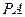 的中点,证明:
的中点,证明: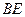 ∥平面
∥平面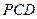 ;
;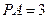 ,求三棱锥
,求三棱锥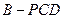 的体积.
的体积.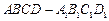 中,
中,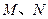 分别为
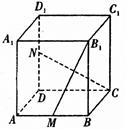
分别为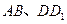 的中点,则异面直线
的中点,则异面直线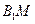 与
与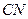 所成角是 ( )
所成角是 ( )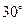
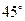
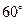
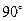
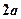 的正方体容器被水充满,首先把半径为
的正方体容器被水充满,首先把半径为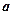 的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )
的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )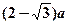
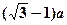
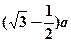
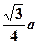
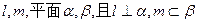 ,给出下列四个命题
,给出下列四个命题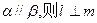 ;②若
;②若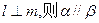 ;③若
;③若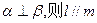 ;④若
;④若