题目内容
已知函数
(1)当 时,求函数
时,求函数 取得最大值和最小值时
取得最大值和最小值时 的值;
的值;
(2)设锐角 的内角A、B、C的对应边分别是
的内角A、B、C的对应边分别是 ,且
,且 ,若向量
,若向量 与向量
与向量 平行,求
平行,求 的值.
的值.
(1) 时,
时, 取得最大值;
取得最大值;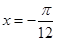 时,
时, 取得最小值.(2)
取得最小值.(2) .
.
解析试题分析:(1)将 解析式降次、化一得
解析式降次、化一得
 ,由于
,由于 ,
, ,将
,将 看作一个整体结合正弦函数的图象可得
看作一个整体结合正弦函数的图象可得 .由
.由 得
得 ,所以
,所以 时,
时, 取得最大值;由
取得最大值;由 得
得 时,
时, 取得最小值.(2)因为向量
取得最小值.(2)因为向量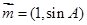 与向量
与向量 平行,所以
平行,所以 即
即 ,又
,又 .由余弦定理得
.由余弦定理得 ,这样根据角C的范围便得边
,这样根据角C的范围便得边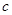 的范围;再据题设
的范围;再据题设 ,即可得
,即可得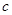 的值.
的值.
(1)
 3分
3分
 4分
4分
所以当 即
即 时,
时, 取得最大值;
取得最大值;
当 即
即 时,
时, 取得最小值 6分
取得最小值 6分
(2)因为向量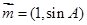 与向量
与向量 平行,所以
平行,所以 即
即
又 .8分
.8分
由余弦定理
因为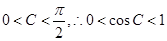 ,
,  即
即
又因为 ,所以
,所以 ,经检验符合三角形要求 12分
,经检验符合三角形要求 12分
考点:1、三角恒等变换;2、向量与三角形.

练习册系列答案
相关题目
 cos
cos cos
cos .
. ,判断函数g(x)的奇偶性,并说明理由.
,判断函数g(x)的奇偶性,并说明理由. 图象的一部分如图所示.
图象的一部分如图所示.
 的解析式;
的解析式; 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值. )(x≠0),且cosα=
)(x≠0),且cosα=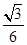 x,求sinα、tanα的值.
x,求sinα、tanα的值. 在
在 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当 时,
时, ;当
;当 时,
时, .(1)求此函数的解析式;(2)求此函数的单调递增区间.
.(1)求此函数的解析式;(2)求此函数的单调递增区间. ,
, .
. 值; (2)求
值; (2)求 的值.
的值.
 x﹣
x﹣ ),x∈R.
),x∈R. ,f(3
,f(3 )=
)=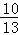 ,f(3β+
,f(3β+ )=
)= .求sin(α+β)的值.
.求sin(α+β)的值. ,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π.
,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π. ,f
,f =
= ,f
,f =-
=- ,求sin(α+β)的值.
,求sin(α+β)的值.