题目内容
已知函数f(x)＝x＋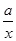
(x≠0，a∈R)．
(1)当a＝4时，证明：函数f(x)在区间[2，＋∞)上单调递增；
(2)若函数f(x)在[2，＋∞)上单调递增，求实数a的取值范围．
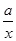(x≠0，a∈R)．(1)当a＝4时，证明：函数f(x)在区间[2，＋∞)上单调递增；
(2)若函数f(x)在[2，＋∞)上单调递增，求实数a的取值范围．
（1）见解析 （2）(－∞，4]．
解：f′(x)＝1－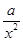
＝
.
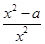(1)证明：当a＝4时，∵x∈[2，＋∞)，
∴x2－4≥0，
∴f′(x)≥0，∴f(x)在[2，＋∞)上单调递增．
(2)若f(x)在[2，＋∞)上单调递增，则f′(x)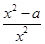＝≥0在[2，＋∞)上恒成立，即a≤x2在[2，＋∞)上恒成立，
∴a≤4，∴实数a的取值范围为(－∞，4]．
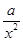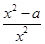＝.(1)证明：当a＝4时，∵x∈[2，＋∞)，
∴x2－4≥0，
∴f′(x)≥0，∴f(x)在[2，＋∞)上单调递增．
(2)若f(x)在[2，＋∞)上单调递增，则f′(x)＝
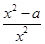≥0在[2，＋∞)上恒成立，即a≤x2在[2，＋∞)上恒成立，∴a≤4，∴实数a的取值范围为(－∞，4]．
练习册系列答案
相关题目
)上单调递减的函数是( )
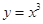
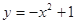
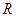且为增函数的是（ ）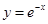
)
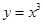
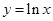
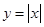
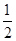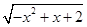的单调递增区间是( )
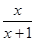)<f(－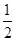
)的解集为________．
＋
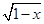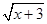的最大值为M，最小值为m，则
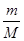的值为( )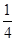
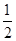
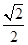
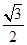
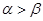，则下列结论正确的是( )
