题目内容
6.小明想利用树影测量他家有房子旁的一棵树的高度,但由于地形的原因,树的影子总有一部分落在墙上,某时刻他测得树留在地面部分的影子长为1.4米,留在墙部分的影高为1.2米,同时,他又测得院子中一个直径为1.2米的石球的影子长(球与地面的接触点和地面上阴影边缘的最大距离)为0.8米,根据以上信息,可求得这棵树的高度是3.3米.(太阳光线可看作为平行光线)分析 画图,设出树的高度,表示出AB,根据三角形相识,确定比例关系求得x.
解答 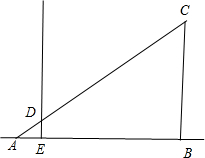
解:如图BC为竿的高度,ED为墙上的影子,BE为地面上的影子.
设BC=x,则根据题意
$\frac{x}{AB}$=$\frac{1.2}{0.8}$,
AB=$\frac{2}{3}$x,
在AE=AB-BE=$\frac{2}{3}$x-1.4,
则$\frac{DE}{BC}$=$\frac{AE}{AB}$,即$\frac{1.2}{x}$=$\frac{\frac{2x}{3}-1.4}{\frac{2x}{3}}$,求得
x=3.3(米)
故树的高度为3.3米,
故答案为:3.3.
点评 本题主要考查了解三角形的实际应用.解题的关键是建立数学模型,把实际问题转化为数学问题.

练习册系列答案
相关题目
16.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个顶点到一条渐近线的距离为$\frac{a}{2}$,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
17.已知cos(θ+π)=-$\frac{1}{3}$,则sin(2θ+$\frac{π}{2}$)=( )
| A. | $\frac{7}{9}$ | B. | $-\frac{7}{9}$ | C. | $\frac{{4\sqrt{2}}}{9}$ | D. | $-\frac{{4\sqrt{2}}}{9}$ |
14.函数 f(x)=(x2-2x)ex的图象大致是( )
| A. | 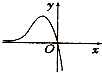 | B. | 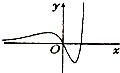 | C. | 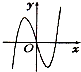 | D. | 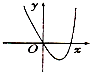 |
18.设等差数列{an}的公差为d.若数列{3${\;}^{{a}_{1}+{a}_{n}}$}为递减数列,则( )
| A. | a1d>0 | B. | a1d<0 | C. | d>0 | D. | d<0 |