题目内容

14．函数 f（x）=（x2-2x）ex的图象大致是（　　）
A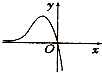．B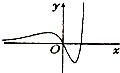．C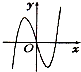．D．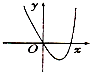

分析 用函数图象的取值，函数的零点，以及利用导数判断函数的图象．

解答 解：由f（x）=0，解得x2-2x=0，即x=0或x=2，
∴函数f（x）有两个零点，∴A，C不正确．
∴f'（x）=（x2-2）ex，
由f'（x）=（x2-2）ex＞0，解得x＞$\sqrt{2}$或x＜-$\sqrt{2}$．
由f'（x）=（x2-2）ex＜0，解得，-$\sqrt{2}$＜x＜$\sqrt{2}$
即x=-$\sqrt{2}$是函数的一个极大值点，
∴D不成立，排除D．
故选：B

点评 本题主要考查函数图象的识别和判断，充分利用函数的性质，本题使用特殊值法是判断的关键，本题的难度比较大，综合性较强．

练习册系列答案
相关题目
4．设f（x）=（1+x）6（1-x）5，则导函数f′（x）中x2的系数是（　　）
A．0B．15C．12D．-15
5．设△ABC的三边a、b、c成等差数列，则tan$\frac{A}{2}$tan$\frac{C}{2}$的值（　　）
A．3B．$\frac{1}{3}$C．$\sqrt{3}$D．$\frac{\sqrt{3}}{3}$
2．在△ABC中，角A、B、C所对的边分别为a、b、c，已知sin（A+$\frac{π}{6}$）+2cos（B+C）=0，
（1）求A的大小；   
（2）若a=6，求b+c的取值范围．
9．以下5个命题：
①对于相关系r|r|越接近1，则线性相关程度越强；
②空间直角坐标系中，（-2，1，9）关于x轴对称的点的坐标（-2，1，9）；
③某人连续投篮投3次，设事件A：至少有一个命中，事件B：都命中，那么事件A与事件B是互斥且不对立的事件；
④推理“半径为r圆的面积S=πr2，则单位圆的面S=π”是类比推理；
⑤定义运算$[\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{ax+cy}\\{bx+dy}\end{array}]$，称$[\begin{array}{l}{x′}\\{y′}\end{array}]$=$[\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$ 为将点（x，y）映到点（x′，y′）的一次变换．若$[\begin{array}{l}{x′}\\{y′}\end{array}]$=$[\begin{array}{l}{2}&{-1}\\{p}&{q}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$把直线y=x上的各点映到这点本身，而把直y=3x上的各点映到这点关于原点对称的点，p=3，q=-2；
其中的真命题是①⑤．（写出所有真命题的序号）
19．在四棱锥P-ABCD中（如图），底面ABCD是直角梯形，M为PC中点，且AB∥DC，又∠ABC=45°，DC=1，AB=2，PA⊥平面ABCD，PA=1．
（Ⅰ）求证：CD∥平面MAB；
（Ⅱ）求三棱锥M-PAD的体；
（Ⅲ）若点K线段PA上，试判断平面KBC和平面PAC的位置关系，并加以证明．
6．小明想利用树影测量他家有房子旁的一棵树的高度，但由于地形的原因，树的影子总有一部分落在墙上，某时刻他测得树留在地面部分的影子长为1.4米，留在墙部分的影高为1.2米，同时，他又测得院子中一个直径为1.2米的石球的影子长（球与地面的接触点和地面上阴影边缘的最大距离）为0.8米，根据以上信息，可求得这棵树的高度是3.3米．（太阳光线可看作为平行光线）
3．设变量x，y满足约束条件$\left\{\begin{array}{l}{y≤2x}\\{x+2y≤2}\\{x≤2}\end{array}\right.$，则z=2x+y的最大值为（　　）
A．8B．6C．4D．$\frac{8}{5}$
4．在等差数列{an}中，Sn为数列{an}的前n项和，若Sn=a，S2n=b，则S3n=3b-3a．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网