题目内容
【题目】2016年6月22 日,“国际教育信息化大会”在山东青岛开幕.为了解哪些人更关注“国际教育信息化大会”,某机构随机抽取了年龄在15-75岁之间的100人进行调查,经统计“青少年”与“中老年”的人数之比为9: 11.
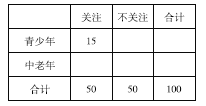
(1)根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查.在这9人中再选取3人进行面对面询问,记选取的3人中关注“国际教育信息化大会”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:参考公式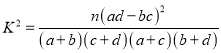 ,其中
,其中![]() .
.
临界值表:
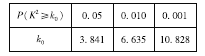
【答案】(1)列联表见解析,有![]() 的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”.
的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”.
(2)分布列见解析, ![]()
【解析】试题分析:(Ⅰ)根据统计数据,可得2×2列联表,根据列联表中的数据,计算K2的值,即可得到结论;
(Ⅱ)ξ的可能取值有0,1,2,3,求出相应的概率,可得ξ的分布列及数学期望.
试题解析:
解:(1)依题意可知,抽取的“青少年”共有![]() 人,“中老年”共有
人,“中老年”共有![]() 人.
人.
完成的![]() 列联表如下:
列联表如下:
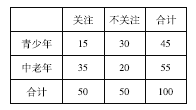
则
![]() ,
,
因为![]() ,所以有
,所以有![]() 的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”.
的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”.
(2)根据题意知选出关注的人数为3,不关注的人数为6,在这9人中再选取3人进行面对面询问, ![]() 的取值可以为0,1,2,3,则
的取值可以为0,1,2,3,则
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
所以![]() 的分布列为
的分布列为
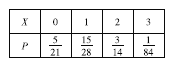
数学期望![]() .
.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目