题目内容
13．已知函数f（x）=x2-2|x|．（1）判断并证明函数的奇偶性；
（2）画出函数图象；
（3）求函数f（x）的值域和单调区间．
分析 （1）函数f（x）=x2-2|x|为偶函数，再利用偶函数的定义进行证明．
（2）化简函数的解析式，作出图象，如图所示：数形结合求得函数f（x）的数值域以及单调增区间．
解答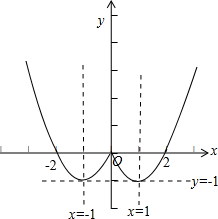 
解：（1）函数f（x）=x2-2|x|为偶函数，证明如下：
函数的定义域为R，关于原点对称，且满足f（-x）=（-x）2-2|-x|=x2-2|x|=f（x），
故函数f（x）=x2-2|x|为偶函数．
（2）函数f（x）=x2-2|x|=$\left\{\begin{array}{l}{{x}^{2}-2x，x≥0}\\{{x}^{2}+2x，x＜0}\end{array}\right.$ 的图象如图所示：
结合函数f（x）的图象可得函数值域为[-1，+∞），
单调增区间为：[-1，0]，[1，+∞），减区间为：（-∞，-1）、（0，1）．
点评 本题主要函数的奇偶性的定义和判断方法，分段函数的应用，作函数的图象，函数的值域和单调性，属于中档题．
练习册系列答案
相关题目
4．曲线$\left\{\begin{array}{l}{x=5cosθ}\\{y=4sinθ}\end{array}\right.$（θ为参数）的离心率是（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{3}{4}$ |
8．
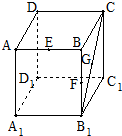有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1，在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G，若此容器可以任意放置，则该容器可装水的最大容积是（ ）
有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1，在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G，若此容器可以任意放置，则该容器可装水的最大容积是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{7}{8}$ | C． | $\frac{11}{12}$ | D． | $\frac{47}{48}$ |