题目内容
17．已知函数f（x+1）是定义在R上的奇函数，若对于任意给定的不等实数x1，x2，不等式（x1-x2）[f（x1）-f（x2）]＞0恒成立，则不等式f（1-x）＜0的解集为（ ）| A． | （1，+∞） | B． | （0，+∞） | C． | （-∞，0） | D． | （-∞，1） |
分析 由（x1-x2）[f（x1）-f（x2）]＞0判断函数f（x）为增函数，结合函数奇偶性和单调性之间的关系进行求解即可．
解答 解：∵（x1-x2）[f（x1）-f（x2）]＞0，
∴函数f（x）为增函数，
∵f（x+1）是定义在R上的奇函数，
∴函数f（x）关于x=1对称，即f（1）=0，
则不等式f（1-x）＜0等价为不等式f（1-x）＜f（1），
即1-x＜1，解得x＞0，
即不等式f（1-x）＜0的解集为（0，+∞），
故选：B
点评 本题主要考查不等式的求解，根据条件判断函数的单调性以及根据函数奇偶性和单调性之间的关系，是解决本题的关键．
练习册系列答案
相关题目
7．若第一象限的点（a，b）关于直线x+y-2=0的对称点在直线2x+y+3=0上，则$\frac{1}{a}+\frac{8}{b}$的最小值是（ ）
| A． | 1 | B． | 3 | C． | $\frac{25}{9}$ | D． | $\frac{17}{9}$ |
8．
已知函数f（x）=sinx?cosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$．
（Ⅰ）化简函数f（x），并用“五点法”画出函数f（x）在长度为一个周期的闭区间上的简图（先在所给的表格中填上所需的数值，再画图）；
（Ⅱ）当x∈[0，$\frac{π}{2}$]时，求函数f（x）的最大值和最小值及相应的x的值．
已知函数f（x）=sinx?cosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$．（Ⅰ）化简函数f（x），并用“五点法”画出函数f（x）在长度为一个周期的闭区间上的简图（先在所给的表格中填上所需的数值，再画图）；
5．若四面体ABCD的棱长都相等，则AB与平面BCD所成角的余弦值等于（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
12．已知函数y=f（x-1）定义域是[-2，3]，则y=f（2x+1）的定义域是（ ）
| A． | $[-2，\frac{1}{2}]$ | B． | [-1，4] | C． | $[-\frac{5}{2}，\frac{5}{2}]$ | D． | [-3，7] |
9．已知展开式（x2-x-2）3（x2+x-2）3=a0+a1x+…+a12x12，则a0+a1的值为（ ）
| A． | 64 | B． | 0 | C． | -64 | D． | 128 |
8．
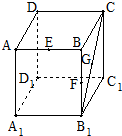有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1，在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G，若此容器可以任意放置，则该容器可装水的最大容积是（ ）
有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1，在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G，若此容器可以任意放置，则该容器可装水的最大容积是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{7}{8}$ | C． | $\frac{11}{12}$ | D． | $\frac{47}{48}$ |