题目内容
20．已知函数f（x）=$\left\{\begin{array}{l}{x-a，x≤0}\\{x+\frac{a}{x}，x＞0}\end{array}\right.$，若f（-1）=-5，则f（2）=4．分析 由分段函数和已知条件可得a值，再代入解析式求解可得．
解答 解：由题意可得f（-1）=-1-a=-5，解得a=4，
∴f（2）=2+$\frac{a}{2}$=4，
故答案为：4．
点评 本题考查函数的值，涉及分段函数，属基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
9．已知展开式（x2-x-2）3（x2+x-2）3=a0+a1x+…+a12x12，则a0+a1的值为（ ）
| A． | 64 | B． | 0 | C． | -64 | D． | 128 |
11．在△ABC中，如果sinA=$\sqrt{3}$sinC，B=$\frac{π}{6}$，角B所对的边b=2，则边c=（ ）
| A． | 1 | B． | $\sqrt{3}$ | C． | 2 | D． | 4 |
8．
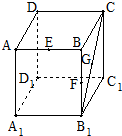有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1，在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G，若此容器可以任意放置，则该容器可装水的最大容积是（ ）
有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1，在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G，若此容器可以任意放置，则该容器可装水的最大容积是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{7}{8}$ | C． | $\frac{11}{12}$ | D． | $\frac{47}{48}$ |
15．已知在△ABC中，若αcosA+bcosB=ccosC，则这个三角形一定是（ ）
| A． | 锐角三角形或钝角三角形 | B． | 以a或b为斜边的直角三角形 | ||
| C． | 以c为斜边的直角三角形 | D． | 等边三角形 |
12．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$+2$\overrightarrow{b}$|=4$\sqrt{2}$，则$\overrightarrow{a}$•$\overrightarrow{b}$的取值范围是（ ）
| A． | （-∞，4] | B． | [4，+∞） | C． | （-∞，2] | D． | [2，+∞） |
9．已知集合A={0，1，x2-5x}，有-4∈A，则实数x的值为（ ）
| A． | 1 | B． | 4 | C． | 1或4 | D． | 36 |