题目内容
19．在等差数列{an}中，a4=18-a5，则数列{an}的前8项的和S8=72．分析 由a4=18-a5，得a4+a5=18，结合等差数列的前n项和公式进行求解．
解答 解：∵a4=18-a5，
∴a4+a5=18，即a1+a8=a4+a5=18，
则数列{an}的前8项的和S8=$\frac{8（{a}_{1}+{a}_{8}）}{2}$=$\frac{8×18}{2}$=72，
故答案为：72．
点评 本题主要考查等差数列前n项和公式的应用，根据等差数列的性质是解决本题的关键．
练习册系列答案
相关题目
8．
已知函数f（x）=sinx?cosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$．
（Ⅰ）化简函数f（x），并用“五点法”画出函数f（x）在长度为一个周期的闭区间上的简图（先在所给的表格中填上所需的数值，再画图）；
（Ⅱ）当x∈[0，$\frac{π}{2}$]时，求函数f（x）的最大值和最小值及相应的x的值．
已知函数f（x）=sinx?cosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$．（Ⅰ）化简函数f（x），并用“五点法”画出函数f（x）在长度为一个周期的闭区间上的简图（先在所给的表格中填上所需的数值，再画图）；
9．已知展开式（x2-x-2）3（x2+x-2）3=a0+a1x+…+a12x12，则a0+a1的值为（ ）
| A． | 64 | B． | 0 | C． | -64 | D． | 128 |
4．曲线$\left\{\begin{array}{l}{x=5cosθ}\\{y=4sinθ}\end{array}\right.$（θ为参数）的离心率是（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{3}{4}$ |
11．在△ABC中，如果sinA=$\sqrt{3}$sinC，B=$\frac{π}{6}$，角B所对的边b=2，则边c=（ ）
| A． | 1 | B． | $\sqrt{3}$ | C． | 2 | D． | 4 |
8．
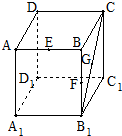有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1，在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G，若此容器可以任意放置，则该容器可装水的最大容积是（ ）
有一容积为1 立方单位的正方体容器ABCD-A1B1C1D1，在棱AB、BB1及对角线B1C的中点各有一小孔E、F、G，若此容器可以任意放置，则该容器可装水的最大容积是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{7}{8}$ | C． | $\frac{11}{12}$ | D． | $\frac{47}{48}$ |
9．已知集合A={0，1，x2-5x}，有-4∈A，则实数x的值为（ ）
| A． | 1 | B． | 4 | C． | 1或4 | D． | 36 |