题目内容
12．已知在△ABC中，∠A：∠B=1：2，∠ACB的平分线CD把△ABC的面积分成3：2两部分，则cosA=（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | 0 |
分析 由A与B的度数之比，得到B=2A，且B大于A，可得出AC大于BC，利用角平分线定理根据角平分线CD将三角形分成的面积之比为3：2，得到BC与AC之比，再利用正弦定理得出sinA与sinB之比，将B=2A代入并利用二倍角的正弦函数公式化简，即可求出cosA的值．
解答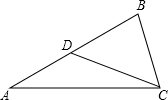 
解：∵A：B=1：2，即B=2A，
∴B＞A，
∴AC＞BC，
∵角平分线CD把三角形面积分成3：2两部分，
∴由角平分线定理得：BC：AC=BD：AD=2：3，
∴由正弦定理$\frac{BC}{sinA}=\frac{AC}{sinB}$得：$\frac{sinA}{sinB}=\frac{2}{3}$，
整理得：$\frac{sinA}{sin2A}=\frac{sinA}{2sinAcosA}$=$\frac{2}{3}$，
则cosA=$\frac{3}{4}$．
故选：C．
点评 此题属于解三角形的题型，涉及的知识有：正弦定理，角平分线定理，以及二倍角的正弦函数公式，熟练掌握定理及公式是解本题的关键．
练习册系列答案
相关题目
20．下列说法正确的是（ ）
| A． | 命题“?x∈R，均有x2-3x-2≥0”的否定是：“?x0∈R，使x02-3x0-2≤0” | |
| B． | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C． | 命题“若x＜y，则x2＜y2”的逆否命题是真命题 | |
| D． | 若命题p∧q为真则命题p∨q一定为真 |