题目内容
3.设a>b>0,点A(a,0),B(-a,0),C(-a,-b),D(a,-b),取线段AB上一点M,找到线段AB上另一点N,使得|AM|,$\frac{1}{2}$|MN|,|NB|成等比数列,设直线DM,CN交于点P.求证:动点P的轨迹就是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的上半部分.分析 由题意设出P(x0,y0)(y0>0),由两点式写出直线CP、DP所在直线方程,求出两直线与x轴的交点坐标,求出|AM|,|MN|,|NB|,结合等比数列的性质列式整理得答案.
解答 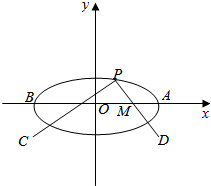 证明:如图,设P(x0,y0)(y0>0),
证明:如图,设P(x0,y0)(y0>0),
则CP所在直线方程:$\frac{y+b}{{y}_{0}+b}=\frac{x+a}{{x}_{0}+a}$,取y=0,得x=$\frac{b{x}_{0}-a{y}_{0}}{{y}_{0}+b}$,∴N($\frac{b{x}_{0}-a{y}_{0}}{{y}_{0}+b}$,0);
DP所在直线方程:$\frac{y+b}{{y}_{0}+b}=\frac{x-a}{{x}_{0}-a}$,取y=0,得x=$\frac{b{x}_{0}+a{y}_{0}}{{y}_{0}+b}$,∴M($\frac{b{x}_{0}+a{y}_{0}}{{y}_{0}+b}$,0).
则|AM|=a-$\frac{b{x}_{0}+a{y}_{0}}{{y}_{0}+b}$=$\frac{ab-b{x}_{0}}{{y}_{0}+b}$,|MN|=$\frac{b{x}_{0}+a{y}_{0}}{{y}_{0}+b}$-$\frac{b{x}_{0}-a{y}_{0}}{{y}_{0}+b}$=$\frac{2a{y}_{0}}{{y}_{0}+b}$,|NB|=$\frac{b{x}_{0}-a{y}_{0}}{{y}_{0}+b}$+a=$\frac{b{x}_{0}+ab}{{y}_{0}+b}$,
由|AM|,$\frac{1}{2}$|MN|,|NB|成等比数列,
得$(\frac{a{y}_{0}}{{y}_{0}+b})^{2}$=$\frac{ab-b{x}_{0}}{{y}_{0}+b}$•$\frac{b{x}_{0}+ab}{{y}_{0}+b}$,
整理得:${a}^{2}{{y}_{0}}^{2}={a}^{2}{b}^{2}-{b}^{2}{{x}_{0}}^{2}$,即$\frac{{{x}_{0}}^{2}}{{a}^{2}}+\frac{{{y}_{0}}^{2}}{{b}^{2}}=1({y}_{0}>0)$.
∴动点P的轨迹就是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的上半部分.
点评 本题考查轨迹方程的求法,考查了等比数列的性质,考查计算能力,属中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{15}{2}$ | B. | $\frac{\sqrt{15}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{3\sqrt{5}}{2}$ |
| A. | 3n | B. | 2n | C. | 3n-1 | D. | 2n-1 |
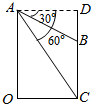
| A. | $\frac{400}{3}$ m | B. | $\frac{400}{3}$$\sqrt{3}$ m | C. | $\frac{200}{3}$$\sqrt{3}$ m | D. | $\frac{200}{3}$ m |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 0 |