题目内容
17.若x∈R,求$\sqrt{(x-5)^{2}+16}$-$\sqrt{(x-1)^{2}+4}$的最大值.分析 $\sqrt{(x-5)^{2}+16}$-$\sqrt{(x-1)^{2}+4}$=$\sqrt{(x-5)^{2}+(0-4)^{2}}$-$\sqrt{(x-1)^{2}+(0-2)^{2}}$,利用其几何意义,可得$\sqrt{(x-5)^{2}+16}$-$\sqrt{(x-1)^{2}+4}$的最大值为(5,4)与(1,2)的距离.
解答 解:$\sqrt{(x-5)^{2}+16}$-$\sqrt{(x-1)^{2}+4}$=$\sqrt{(x-5)^{2}+(0-4)^{2}}$-$\sqrt{(x-1)^{2}+(0-2)^{2}}$,
表示点(x,0)与点(5,4)的距离减去点(x,0)与点(1,2)的距离,
∴$\sqrt{(x-5)^{2}+16}$-$\sqrt{(x-1)^{2}+4}$的最大值为(5,4)与(1,2)的距离,即$\sqrt{(5-1)^{2}+(4-2)^{2}}$=2$\sqrt{5}$.
点评 本题考查求$\sqrt{(x-5)^{2}+16}$-$\sqrt{(x-1)^{2}+4}$的最大值,正确理解其几何意义是关键.

练习册系列答案
相关题目
8.在200m高的山顶上,测得山下一塔顶与塔底的俯角分别是30°,60°,如图所示则塔高CB为( ) 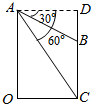

| A. | $\frac{400}{3}$ m | B. | $\frac{400}{3}$$\sqrt{3}$ m | C. | $\frac{200}{3}$$\sqrt{3}$ m | D. | $\frac{200}{3}$ m |
5.在△ABC中,若(a+b+c)(c+b-a)-bc=0,则∠A=( )
| A. | 120° | B. | 150° | C. | 60° | D. | 30° |
12.已知在△ABC中,∠A:∠B=1:2,∠ACB的平分线CD把△ABC的面积分成3:2两部分,则cosA=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 0 |
9.下列命题中,真命题是( )
| A. | ?x0∈R,2x≤0 | B. | ?x∈R,log2x>0 | ||
| C. | a+b=0的充要条件是$\frac{a}{b}$=-1 | D. | a>0、b>0是ab>0的充分条件 |