题目内容
4.城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客的需求,为此,某城市公交公司在某站台随机调查了80名乘客,他们的候车时间如下所示(单位:min):17 14 20 12 10 24 18 17 1 22 13 19 28 5 34 7
25 18 28 1 15 31 12 11 10 16 12 9 10 13 19 10
12 12 16 22 17 23 16 15 16 11 9 3 13 2 18 22
19 9 23 28 15 21 28 12 11 14 15 3 11 6 2 18
25 5 12 15 20 16 12 28 20 12 28 15 8 32 18 9
(1)将数据进行适当的分组,并画出相应的频率分布直方图和频率折线图;
(2)这80名乘客候车时间的平均数是多少?标准差呢?
(3)你能为公交公司提出什么建议?
分析 (1)计算极差、确定组距并分组,列出频率分布表,画出频率分布直方图与折线图;
(2)根据频率分布直方图,计算这组数据的平均数与方差、标准差;
(3)根据频率分布直方图与折线图,结合平均数与标准差,得出统计结论与建议.
解答 解:(1)计算极差为34-1=33,
确定组距为6,分为6组,
列出频率分布表,如下;
| 组别 | 候车时间 | 频数 | 频率 |
| 一 | [0,6) | 8 | $\frac{1}{10}$ |
| 二 | [6,12) | 15 | $\frac{3}{16}$ |
| 三 | [12,18) | 28 | $\frac{7}{20}$ |
| 四 | [18,24) | 17 | $\frac{17}{80}$ |
| 五 | [24,30) | 9 | $\frac{9}{80}$ |
| 六 | [30,36] | 3 | $\frac{3}{80}$ |
| 合计 | 80 | 1.00 |

根据频率分布直方图,画出对应的折线图如图所示;
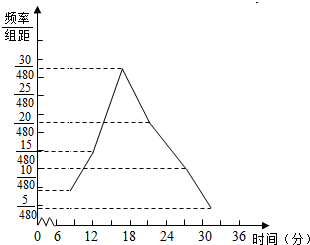
(2)根据频率分布直方图,计算这80名乘客等车时间的平均数为
3×$\frac{1}{10}$+9×$\frac{3}{16}$+15×$\frac{7}{20}$+21×$\frac{17}{80}$+27×$\frac{9}{80}$+33×$\frac{3}{80}$≈16(分钟),
计算这组数据的方差为
s2=$\frac{1}{10}$×(3-16)2+$\frac{3}{16}$×(9-16)2+$\frac{7}{20}$×(15-16)2+$\frac{17}{80}$×(21-16)2+$\frac{9}{80}$×(27-16)2+$\frac{3}{80}$×(33-16)2=29.375,
标准差为s≈5.4;
(3)根据频率分布直方图与折线图,结合平均数与标准差,得
乘客等公交车的时间多集中在12~30分钟之间,并且平均等车时间为16分钟,等车时间的波动性较大;
建议公交公司发车时间应间隔均匀,尽量缩短发车时间间隔.
点评 本题考查了频率分布直方图与折线图的应用问题,也考查了平均数与方差、标准差的计算问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知在△ABC中,∠A:∠B=1:2,∠ACB的平分线CD把△ABC的面积分成3:2两部分,则cosA=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 0 |
19.已知集合A={1,3,9},B={1,9},则A∪B=( )
| A. | {1,3,9} | B. | {1,9} | C. | {3} | D. | {3,9} |
9.下列命题中,真命题是( )
| A. | ?x0∈R,2x≤0 | B. | ?x∈R,log2x>0 | ||
| C. | a+b=0的充要条件是$\frac{a}{b}$=-1 | D. | a>0、b>0是ab>0的充分条件 |
16.已知结合A={x|y=$\sqrt{x+1}$},集合B={y|y=sinx},则下列结论正确的是( )
| A. | A∩B=∅ | B. | A∪B=B | C. | A∩B=A | D. | B?A |