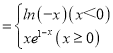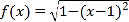题目内容
【题目】在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ2(cos2θ+3sin2θ)=12,直线l的参数方程为![]() (t为参数),直线l与曲线C交于M,N两点.
(t为参数),直线l与曲线C交于M,N两点.
(1)若点P的极坐标为(2,π),求|PM||PN|的值;
(2)求曲线C的内接矩形周长的最大值.
【答案】(1)![]() (2)16
(2)16
【解析】
(1)利用极坐标转化为直角坐标的公式,求得曲线![]() 的直角坐标方程.求得
的直角坐标方程.求得![]() 的直角坐标,由此判断
的直角坐标,由此判断![]() 在直线
在直线![]() 上,求得直线
上,求得直线![]() 的标准参数方程,代入曲线
的标准参数方程,代入曲线![]() 的直角坐标方程,化简后写出韦达定理,结合直线参数的几何意义,求得
的直角坐标方程,化简后写出韦达定理,结合直线参数的几何意义,求得![]() 的值.
的值.
(2)求得椭圆![]() 内接矩形周长的表达式,结合三角函数最值的求法,求得周长的最大值.
内接矩形周长的表达式,结合三角函数最值的求法,求得周长的最大值.
(1)曲线C的极坐标方程为ρ2(cos2θ+3sin2θ)=12,转换为直角坐标方程为![]() .
.
点P的极坐标为(2,π),转换为直角坐标为(﹣2,0)由于点P(﹣2,0)在直线l上,
所以直线l的参数方程为![]() (t为参数),转化为
(t为参数),转化为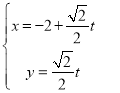 (t为参数),
(t为参数),
所以代入曲线的方程为![]() ,
,
整理得![]() ,
,
所以|PM||PN|=|t1t2|=4.
(2)不妨设Q(![]() ),(
),(![]() ),
),
所以该矩形的周长为4(![]() )=16sin(
)=16sin(![]() ).
).
当![]() 时,矩形的周长的最大值为16.
时,矩形的周长的最大值为16.

练习册系列答案
相关题目