题目内容

8．已知m∈R，n∈R，并且m+3n=1，则em+e3n的最小值$2\sqrt{e}$．

分析 根据题意、指数的运算和基本不等式求出em+e3n的最小值即可．

解答 解：因为m+3n=1，所以em+e3n≥2$\sqrt{{e}^{m+3n}}$=$2\sqrt{e}$，
当且仅当em=e3n时取等号，
所以em+e3n的最小值是$2\sqrt{e}$，
故答案为：$2\sqrt{e}$．

点评 本题考查了基本不等式求最值，以及指数的运算性质，属于基础题．

练习册系列答案
相关题目
20．设$\overrightarrow a，\overrightarrow b，\overrightarrow c$是单位向量，且$\overrightarrow a•\overrightarrow b=0，则（{\overrightarrow a+\overrightarrow c}）•（{\overrightarrow b+\overrightarrow c}）$的最大值为$\sqrt{2}+1$．
19．已知等差数列{an}的公差d＞0，前n项和为Sn，且a1=2，S2•S3=$\frac{112}{3}$．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若从{an}中抽取一个公比为q的等比数列{a${\;}_{{k}_{n}}$}，其中k1=1，且k1＜k2＜…＜kn＜…，kn∈N*，求满足条件的最小q值．
16．等比数列{an}的前n 项和为Sn，已知S1，S3，S2成等差数列
（1）求{an}的公比q；
（2）若a1-a3=3，bn=nan．求数列{bn}的前n 项和Tn．
3．已知函数f（x）=$\frac{sinx}{{e}^{x}}$．
（1）求函数f（x）的单调区间；
（2）如果对于任意的x∈[-$\frac{π}{2}$，0]，f（x）≤kx恒成立，求实数k的取值范围．
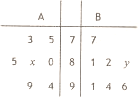13．某学校从A、B两个班级中各选出7名学生参加市级比赛，他们去得的成绩（满分100分）的茎叶如图所示，其中A班学生成绩的众数是85，B班学生成绩的中位数是83．则x+y的值为8．
20．一个几何体的三视图如图所示（单位：m），则该几何体的表面积为（单位：m2）（　　）
A．（11+$4\sqrt{2}$）πB．（12+4$\sqrt{2}$）πC．（13+4$\sqrt{2}$）πD．（14+4$\sqrt{2}$）π
17．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的右顶点、上顶点分别为A、B，坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$，且$a=\sqrt{2}b$．
（1）求椭圆C的方程；
（2）过椭圆C的左焦点F1的直线l交椭圆于M、N两点，且该椭圆上存在点P，使得四边形MONP（图形上的字母按此顺序排列）恰好为平行四边形，求直线l的方程．
18．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为6．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网