题目内容
9.已知函数f(x)=cos($\frac{aπ}{3}$x),a为抛掷一颗骰子所得的点数,则函数f(x)在[0,4]上零点的个数小于5或大于6的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{3}$ |
分析 求出函数f(x)=cos($\frac{aπ}{3}$x)的周期,根据函数f(x)在[0,4]上零点的个数小于5或大于6,求出a的值,即可求出概率.
解答 解:函数f(x)=cos($\frac{aπ}{3}$x)的周期为T=$\frac{2π}{\frac{aπ}{3}}=\frac{6}{a}$,∵函数f(x)在[0,4]上零点的个数小于5或大于6,
∴a=1、2、3、5、6.
共计5个,
故函数f(x)在[0,4]上零点的个数小于5或大于6的概率为$\frac{5}{6}$.
故选B.
点评 本题考查概率是计算,确定a的值是关键,属于基础题

练习册系列答案
相关题目
20.一个几何体的三视图如图所示(单位:m),则该几何体的表面积为(单位:m2)( )


| A. | (11+$4\sqrt{2}$)π | B. | (12+4$\sqrt{2}$)π | C. | (13+4$\sqrt{2}$)π | D. | (14+4$\sqrt{2}$)π |
1.四棱锥S-ABCD中,底面ABCD是边长为2$\sqrt{3}$的正方形,SA⊥平面ABCD,且SA=2$\sqrt{6}$,则此四棱锥的外接球的表面积为( )
| A. | 12π | B. | 24π | C. | 144π | D. | 48π |
19.设全集U={1,2,3,4,5,6,7},P={1,2,3,4},Q={3,4,5,6},则P∩(∁UQ)=( )
| A. | {1,2,3,4,5,6} | B. | {1,2,3,4,5} | C. | {1,2,5} | D. | {1,2} |
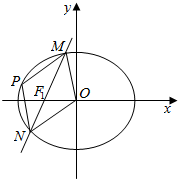 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$,且$a=\sqrt{2}b$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$,且$a=\sqrt{2}b$.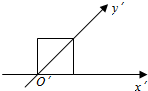 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$.
用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个边长为1的正方形,则原来的图形的面积是2$\sqrt{2}$.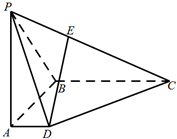 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,∠DAB=90°,PA=AB=BC=3,AD=1. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为6.
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为6.