题目内容
以下有四种说法,其中正确说法的个数为:
(1)命题“若 ”,则“
”,则“ ”的逆命题是真命题
”的逆命题是真命题
(2)“ ”是“
”是“ ”的充要条件;
”的充要条件;
(3) “ ”是“
”是“ ”的必要不充分条件;
”的必要不充分条件;
(4)“ ”是“
”是“ ”的必要不充分条件.
”的必要不充分条件.
| A.0个 | B.1个 | C.2个 | D.3个 |
A
解析试题分析:(1)命题“若 ”,则“
”,则“ ”的逆命题是:若
”的逆命题是:若 ,则
,则 ,逆命题是假命题,因为m=0时不成立;
,逆命题是假命题,因为m=0时不成立;
(2)“ ”是“
”是“ ”的充要条件,错误,比如0>-5,但02不大约(-5)2;
”的充要条件,错误,比如0>-5,但02不大约(-5)2;
(3) “ ”是“
”是“ ”的必要不充分条件,错误,应该是充分不必要条件;
”的必要不充分条件,错误,应该是充分不必要条件;
(4)“ ”是“
”是“ ”的必要不充分条件,错误,
”的必要不充分条件,错误, 只说明
只说明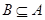 ,和集合A是不是空集没什么关系,因此是既不充分也不必要条件。
,和集合A是不是空集没什么关系,因此是既不充分也不必要条件。
考点:命题真假的判断;四种命题;充分、必要、充要条件的判断。
点评:判断命题真假的时候,我们一定要注意特殊情况,对于不成立的命题,可以举反例说明。属于基础题型。

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
下列命题中,是真命题的是( )
A. ∈R , ∈R , |
B.  |
C. ∈ ∈  |
D. ∈ ∈ |
已知 都是实数,且
都是实数,且 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
a<0是方程 至少有一个负数根的( )
至少有一个负数根的( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列有关命题的说法正确的是
A.命题“若 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ” ” |
B.“若 ,则 ,则 , , 互为相反数”的逆命题为真命题 互为相反数”的逆命题为真命题 |
C.命题“ ,使得 ,使得 ”的否定是:“ ”的否定是:“ ,均有 ,均有 ” ” |
D.命题“若 ,则 ,则 ”的逆否命题为真命题 ”的逆否命题为真命题 |
下列有关命题的说法正确的是( )
A.命题 “若 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ” ” |
B.“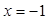 ”是“ ”是“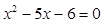 ”的必要不充分条件 ”的必要不充分条件 |
C.命题“存在 , 使得 , 使得 ”的否定是:“对任意 ”的否定是:“对任意 , 均有 , 均有 ” ” |
D.命题“若 ,则 ,则 ”的逆否命题为真命题 ”的逆否命题为真命题 |
命题“若α= ,则tanα=1”的逆否命题是( )
,则tanα=1”的逆否命题是( )
A.若α≠ ,则tanα≠1 ,则tanα≠1 | B.若α= ,则tanα≠1 ,则tanα≠1 |
C.若tanα≠1,则α≠ | D.若tanα≠1,则α= |
已知 为两个命题,则“
为两个命题,则“ 是真命题”是 “
是真命题”是 “ 是真命题”的( )
是真命题”的( )
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |


