题目内容
下列有关命题的说法正确的是
A.命题“若 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ” ” |
B.“若 ,则 ,则 , , 互为相反数”的逆命题为真命题 互为相反数”的逆命题为真命题 |
C.命题“ ,使得 ,使得 ”的否定是:“ ”的否定是:“ ,均有 ,均有 ” ” |
D.命题“若 ,则 ,则 ”的逆否命题为真命题 ”的逆否命题为真命题 |
B
解析试题分析:若xy=0,则x=0的否命题为:若xy≠0,则x≠0;若x+y=0,则x,y互为相反数的逆命题为真命题为若x,y互为相反数,则x+y=0;?x∈R,使得2x2-1<0的否定是:“?x∈R,均有2x2-1≥0;若cosx=cosy,则x=y为假命题,则根据互为逆否命题的真假相同可知逆否命题为假命题
解:若xy=0,则x=0的否命题为:若xy≠0,则x≠0,故A错误
若x+y=0,则x,y互为相反数的逆命题为真命题为若x,y互为相反数,则x+y=0,为真命题
?x∈R,使得2x2-1<0的否定是:“?x∈R,均有2x2-1≥0,故C错误
若cosx=cosy,则x=y为假命题,则根据互为逆否命题的真假相同可知逆否命题为假命题,故D错误
故选B
考点:本题主要考查了命题真假相同的判断。
点评:解题中主要涉及到了,命题的逆命题、否命题、逆否命题的写法及互为逆否命题的真假关系的应用。即互为逆否命题的真假相同,属于基础题。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
设命题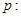 非零向量
非零向量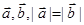 是
是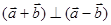 的充要条件;命题
的充要条件;命题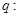 “
“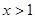 ”是“
”是“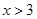 ”的充要条件,则( )
”的充要条件,则( )
A.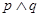 为真命题 为真命题 | B.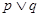 为假命题 为假命题 |
C.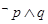 为假命题 为假命题 | D.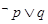 为真命题 为真命题 |
命题“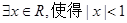 ”的否定是 ( )
”的否定是 ( )
A.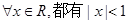 | B.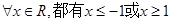 |
C.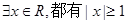 | D.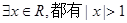 |
“|x|<1”是“ <0”的
<0”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 ,
, ,
,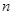 均为直线,其中
均为直线,其中 ,
,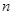 在平面
在平面 内,“
内,“ ”是“
”是“ 且
且 ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
以下有四种说法,其中正确说法的个数为:
(1)命题“若 ”,则“
”,则“ ”的逆命题是真命题
”的逆命题是真命题
(2)“ ”是“
”是“ ”的充要条件;
”的充要条件;
(3) “ ”是“
”是“ ”的必要不充分条件;
”的必要不充分条件;
(4)“ ”是“
”是“ ”的必要不充分条件.
”的必要不充分条件.
| A.0个 | B.1个 | C.2个 | D.3个 |
设P: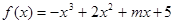 在(-∞,+∞)内单调递减,q:
在(-∞,+∞)内单调递减,q: ,则P是q的( )
,则P是q的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
 满足
满足 则
则 ;
;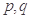 ,若
,若 为真,则
为真,则 为真;
为真; ,若
,若 ,则
,则 ;
; 与直线
与直线 垂直,则
垂直,则 .
. ,则
,则 ”的逆否命题为假命题;
”的逆否命题为假命题; .则
.则 ,使
,使 ;
; ”是“函数
”是“函数 为偶函数”的充要条件;
为偶函数”的充要条件; “
“ ,使
,使 ”;命题
”;命题 “若
“若 ,则
,则 ”,那么
”,那么 为真命题.其中正确的个数是( )
为真命题.其中正确的个数是( )