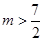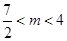题目内容
如图:在面积为1的DPMN中,tanÐPMN=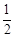 ,tanÐMNP=-2,试建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程。
,tanÐMNP=-2,试建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程。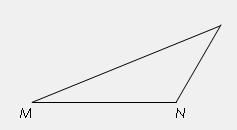
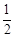 ,tanÐMNP=-2,试建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程。
,tanÐMNP=-2,试建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程。
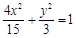
【错解分析】通过建立恰当的直角坐标系,将实际问题转化成解析几何问题来求解依题意:
坐标系的选择是显然的,(如图),从而椭圆方程为:
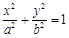 ,以下所要解决的问题就是怎样根据题目的条件来确定a、b了(待定系数法)。
,以下所要解决的问题就是怎样根据题目的条件来确定a、b了(待定系数法)。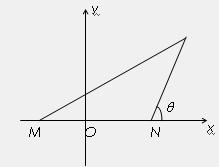
【正解】如图:以MN所在直线为x轴,MN的垂直平分线为y轴建立直角坐标系。

设以M、N为焦点且过点P的椭圆方程为:
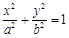 (a>b>0),
(a>b>0),焦点为M(-c,0),N(c,0)(c>0)。由tanÐPMN=
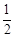 ,tanÐMNP=-2知:直线MP的斜率为
,tanÐMNP=-2知:直线MP的斜率为 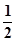 ,直线PN的斜率为2所以直线MP、NP的方程分别为:
,直线PN的斜率为2所以直线MP、NP的方程分别为: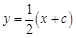 和y=2(x-c)将此两方程联立解得:
和y=2(x-c)将此两方程联立解得: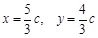 ,即P点的坐标为
,即P点的坐标为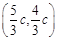 。在DMNP中,|MN|=2c,MN边上的高即为P点的纵坐标
。在DMNP中,|MN|=2c,MN边上的高即为P点的纵坐标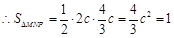
解得
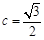 ,即P点坐标为
,即P点坐标为 。再由两点间距离公式求得:
。再由两点间距离公式求得: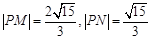 由椭圆的定义可得:
由椭圆的定义可得: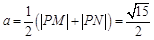 。又:
。又: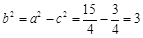 故:所求椭圆的方程为:
故:所求椭圆的方程为: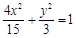 。
。
练习册系列答案
相关题目
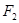 为一个焦点的椭圆,近地点A距地面为
为一个焦点的椭圆,近地点A距地面为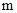 千米,远地点B距地面为
千米,远地点B距地面为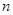 千米,地球半径为
千米,地球半径为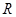 千米,则飞船运行轨道的短轴长为( )
千米,则飞船运行轨道的短轴长为( )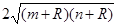
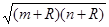
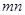
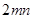
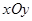 中,
中,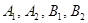 为椭圆
为椭圆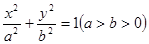 的四个顶点,F为其右焦点,直线
的四个顶点,F为其右焦点,直线 与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为
与直线B1F相交于点T,线段OT与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为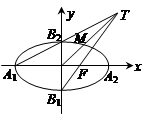
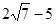
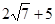
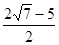
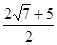
 。
。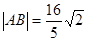 ,求直线l的方程。
,求直线l的方程。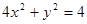 上,求
上,求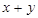 的最大、最小值.
的最大、最小值.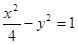 的两个焦点,点在双曲线上且满足
的两个焦点,点在双曲线上且满足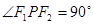 ,则
,则 的面积是( )。
的面积是( )。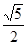
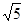
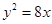 的准线
的准线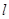 与双曲线
与双曲线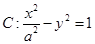 相切,则双曲线
相切,则双曲线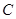 的离心率
的离心率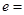 .
. 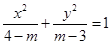 表示焦点在
表示焦点在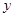 轴上的椭圆,则
轴上的椭圆,则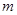 的取值范围是
的取值范围是