题目内容
8.已知直线l过点(0,-1),且直线y=-x+2垂直,则直线l的方程为x-y-1=0.分析 根据直线l与直线y=-x+2垂直,设出l的方程,利用点的坐标求出未知系数.
解答 解:∵直线l过点(0,-1),且直线y=-x+2垂直,
设直线l的方程为y=x+b,
∴-1=0+b,
解得b=-1,
∴直线l的方程为y=x-1,
化为一般方程是x-y-1=0.
故答案为:x-y-1=0.
点评 本题考查了直线方程的应用问题,也考查了两条直线垂直、斜率之积等于-1的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.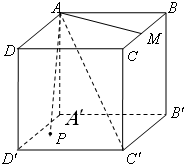 如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
 如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )| A. | 一段圆弧 | B. | 一段椭圆弧 | C. | 一段双曲线弧 | D. | 一段抛物线弧 |
16.设i是虚数单位,若复数$z=\frac{{{a^2}+ai}}{1-i}>0$,则a的值为( )
| A. | 0或-1 | B. | 0或1 | C. | -1 | D. | 1 |
20.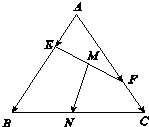 如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )
如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )
 如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )
如图,在边长为1的正三角形ABC中,E,F分别为边AB,AC上的动点,且满足$\overrightarrow{AE}$=m$\overrightarrow{AB}$,$\overrightarrow{AF}$=n$\overrightarrow{AC}$,其中m,n∈(0,1),m+n=1,M,N分别是EF,BC的中点,则|$\overrightarrow{MN}$|的最小值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{5}{3}$ |
17.已知$\frac{a+3i}{i}$=b+i(a,b∈R,i为虚数单位),则a+b等于( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
18.若向量$\overrightarrow{a}$=(2,x+1),$\overrightarrow{b}$=(x+2,6),又$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为锐角,则实数x的取值范围为( )
| A. | {x|x>-$\frac{5}{4}$且x≠2} | B. | {x|x>-$\frac{5}{4}$} | C. | {x|x<-$\frac{5}{4}$且x≠-5} | D. | {x|x<-$\frac{5}{4}$} |
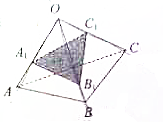 如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OC=4,OB=3.
如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OC=4,OB=3.